题目内容
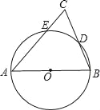
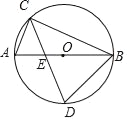
【题目】已知:如图,在梯形ABCD中,AD∥BC,AB=DC,E是对角线AC上一点,且AC·CE=AD·BC.
(1)求证:∠DCA=∠EBC;
(2)延长BE交AD于F,求证:AB2=AF·AD.

【答案】(1)见解析;(2)见解析.
【解析】
(1)由AD∥BC得∠DAC=∠BCA, 又∵AC·CE=AD·BC∴![]() ,∴△ACD∽△CBE ,
,∴△ACD∽△CBE ,
∴∠DCA=∠EBC,
(2)由题中条件易证得△ABF∽△DAC∴![]() ,又∵AB=DC,∴
,又∵AB=DC,∴![]()
证明:

(1)∵AD∥BC,
∴∠DAC=∠BCA,
∵AC·CE=AD·BC,
∴![]() ,
,
∴△ACD∽△CBE ,
∴∠DCA=∠EBC,
(2)∵AD∥BC,
∴∠AFB=∠EBC,
∵∠DCA=∠EBC,
∴∠AFB=∠DCA,
∵AD∥BC,AB=DC,
∴∠BAD=∠ADC,
∴△ABF∽△DAC,
∴![]() ,
,
∵AB=DC,
∴![]() .
.

练习册系列答案
相关题目