题目内容
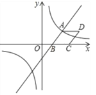
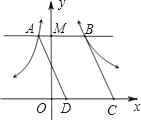
【题目】如图，过y轴上一个动点M作x轴的平行线，交双曲线y=
于点A，交双曲线
于点B，点C、点D在x轴上运动，且始终保持DC＝AB，则平行四边形ABCD的面积是（ ）
A. 7 B. 10 C. 14 D. 28
【答案】C.
【解析】
试题设出M点的坐标，可得出过M与x轴平行的直线方程为y=m，将y=m代入反比例函数y=
中，求出对应的x的值，即为A的横坐标，将y=m代入反比例函数y=
中，求出对应的x的值，即为B的横坐标，用B的横坐标减去A的横坐标求出AB的长，根据DC=AB，且DC 与AB平行，得到四边形ABCD是平行四边形，过B作BN垂直于x轴，平行四边形底边为DC，DC边上的高为BN，由B的纵坐标为ｍ得到BN=m，再由求出的AB的长，得到DC的长，利用平行四边形的面积等于底乘以高可得出平行四边形ABCD的面积.
试题解析：设M的坐标为（0，m）（m＞0）则直线AB的方程为：y=m，
将y=m代入y=中得：
，∴A（
，m）
将y=m代入y=中得：
，∴B（
，m）
∴DC=AB=-（）=
过B作BN⊥x轴，则有BN=m，
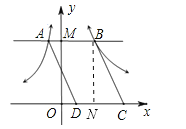
则平行四边形ABCD的面积S=DC·BN=×m=14.
故选C.
练习册系列答案
考前必练系列答案
相关题目
