题目内容
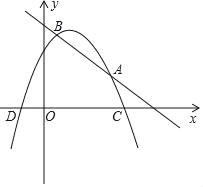
【题目】已知抛物线y=﹣x2+bx+c与直线y=﹣x+m相交于第一象限内不同的两点A(4,n),B(1,4),
(1)求此抛物线的解析式.
(2)抛物线上是否存点P,使直线OP将线段AB平分?若存在直接求出P点坐标;若不存在说明理由.
【答案】(1)y=-x2+4x+1(2)存在点P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() )
)
【解析】
(1)根据待定系数法求出m、n的值,然后根据待定系数法求出二次函数的解析式;
(2)根据平分线段AB求出AB的中点M,然后求出OM的解析式,构造方程组求解即可.
(1)∵点B(1,4)在y=-x+m上
∴4=-1+m
解得m=5
∴y=-x+5
∵A(4,n)在直线y=-x+5上
∴n=-4+5=1
即A为(4,1)
∴![]()
解得![]()
∴抛物线的解析式为:y=-x2+4x+1

(2)存在
由(1)知:AB的中点M为(![]() ,
,![]() )
)
∴直线OM为y=x
因此可得![]()
解得 或
或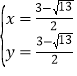
即存在点P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ).
).

练习册系列答案
相关题目