��Ŀ����
����Ŀ������ȫ�ȵ�ֱ�������� ABC �� DEF �ص���һ�����С�A=60�㣬AC=1���̶���ABC ����������DEF �������²�����
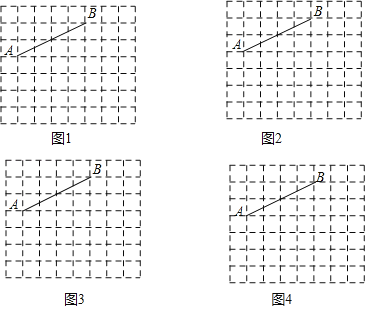
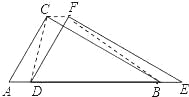
��1����ͼ����DEF ���߶� AB ����ƽ�ƣ��� D �����߶� AB ���ƶ��������� DC��CF��FB���ı��� CDBF ����״�ڲ��ϵı仯��������������仯��������������
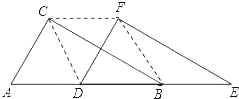
��2����ͼ���� D ���Ƶ� AB ���е�ʱ����������ı���CDBF ����״����˵�����ɣ�
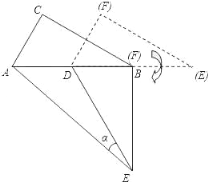
��3����ͼ����DEF �� D ��̶��� AB ���е㣬Ȼ���� D �㰴˳ʱ�뷽����ת��DEF��ʹ DF ���� AB ���ϣ���ʱ F ��ǡ���� B ���غϣ����� AE��������� sin����ֵ��
���𰸡���1������C��CG��AB��G
��Rt��ACG�� �ߡ�A��60��
��sin60����![]() ��
��![]() ����������1��
����������1��
��Rt��ABC�� ��ACB��90���ABC��30��
��AB=2 ��������������������������������2��
��![]() ������3��
������3��
��2������������������������������������4��
��D��AB���е� ��AD=DB=CF=1
��Rt��ABC��CD������� ��CD=1����5��
ͬ�� BF=1 ��CD=DB=BF=CF
���ı���CDBF��������������������������6��
��3����Rt��ABE��![]()
��![]() ����������������������7��
����������������������7��
����D��DH��AE ����ΪH
����ADH�ס�AEB ��![]()
��![]() �� DH=
�� DH=![]() ����8��
����8��
��Rt��DHE��
sin��=![]() =��=
=��=![]() ��������������9��
��������������9��
��������
��1������ƽ�Ƶ����ʵõ�AD=BE���ٽ������ƽ����ľ�����ȣ���������ACD���������������BEF�����������Ҫ������ε��������������ABC�����������60�ȵ�ֱ��������ABC��AC=1���������BC�ij����Ӷ�����������
��2������ֱ��������б���ϵ����ߵ���б�ߵ�һ���ƽ�Ƶ����ʣ����ɵõ����ı��ε������߶���ȣ�������һ�����Σ�
��3����D����DH��AE��H������Ҫ��Ľǹ��쵽ֱ���������У�����������ADE������IJ�ͬ���㷽�����������DH�ij���������⣮

 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�