题目内容
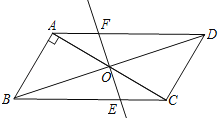
【题目】已知,如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)求证:当旋转角为90°时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如能,说明理由并求出此时AC绕点O顺时针旋转的度数.
【答案】(1)见解析 (2)见解析
【解析】
(1)根据∠BAC=∠AOF=90°推出AB∥EF,根据平行四边形性质得出AF∥BE,即可推出四边形ABEF是平行四边形;
(2)证△DFO≌△BEO,推出OF=OE,得出四边形BEDF是平行四边形,根据勾股定理求出AC,求出OA=AB=1,求出∠AOB=45°,根据∠AOF=45°,推出EF⊥BD,根据菱形的判定推出即可.
(1)证明:∵∠AOF=90°,∠BAO=90°,
∴AB∥EF,
又∵平行四边形ABCD,
∴AF∥EB,
∴四边形ABEF是平行四边形;
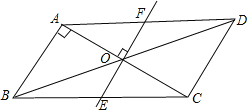
(2)当旋转角∠AOF=45°时,四边形BEDF是菱形,理由如下:
∵平行四边形ABCD,
∴AD∥BC,BO=DO,
∴∠FDO=∠EBO,∠DFO=∠BEO,
在△DFO和△BEO中
∵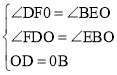 ,
,
∴△DFO≌△BEO(AAS),
∴OF=OE,
∴四边形BEDF是平行四边形,
∵AB=1,BC=![]() ,
,
∴在Rt△BAC中,由勾股定理得:AC=2,
∴AO=1=AB,
∴∠AOB=45°,
又∵∠AOF=45°,
∴∠BOF=90°,
∴BD⊥EF,
∴四边形BEDF是菱形,
即在旋转过程中,四边形BEDF能是菱形,此时AC绕点O顺时针旋转的度数是45°.


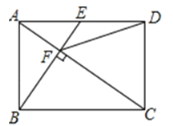
【题目】在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,对于结论①CF=2AF②△AEF∽△CAB③DF=DC④tan∠CAD=![]() 正确的有_______________.
正确的有_______________.
【题目】为了节约用水,某水厂规定:某单元居民如果一个月的用水量不超过![]() 吨,那么这个月该单元居民只交10元水费.如果超过
吨,那么这个月该单元居民只交10元水费.如果超过![]() 吨,则这个月除了仍要交10元水费外,超过那部分按每吨
吨,则这个月除了仍要交10元水费外,超过那部分按每吨![]() 元交费.
元交费.
(1)该单元居民8月份用水80吨,超过了“规定的![]() 吨”,则超过部分应交水费 (80-x)
吨”,则超过部分应交水费 (80-x)
元(用含x的式子表示).
(2)下表是该单元居民9月、10月的用水情况和交费情况:
月份 | 用水量(吨) | 交费总数(元) |
9月份 | 85 | 25 |
10月份 | 50 | 10 |
根据上表数据,求该x吨是多少?