题目内容
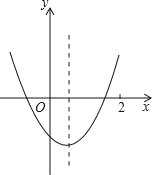
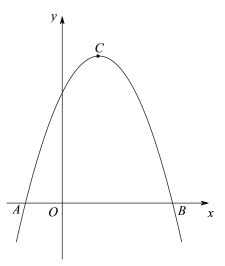
【题目】如图,在平面直角坐标系xOy中,二次函数![]() (a、b都是常数,且a<0)的图像与x轴交于点
(a、b都是常数,且a<0)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的解析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当∠PBA=∠CBD时,求点P的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)由点A,B的坐标,利用待定系数法即可求出二次函数的解析式,再利用配发法即可求出顶点C的坐标;
(2)利用一次函数图象上点的坐标特征可求出点D的坐标,过点D作DE⊥BC,垂足为点E,设抛物线对称轴与x轴的交点为点F,由点B,C,D,F的坐标可得出CD,DF,BF的长,利用勾股定理可得出BC的长,利用角的正切值不变可求出DE的长,进而可求出BE的长,再利用余切的定义即可求出∠CBD的余切值;
(3)设直线PB与y轴交于点M,由∠PBA=∠CBD及∠CBD的余切值可求出OM的长,进而可得出点M的坐标,由点B,M的坐标,利用待定系数法即可求出直线BP的解析式,联立直线BP及二次函数解析式成方程组,通过解方程组可求出点P的坐标.
(1)将A(-2,0),B(6,0)代入y=ax2+bx+6,得:![]() ,
,
解得: ,
,
∴二次函数的解析式为y=-![]() x2+2x+6,
x2+2x+6,
∵y=-![]() x2+2x+6=-
x2+2x+6=-![]() (x-2)2+8,
(x-2)2+8,
∴点C的坐标为(2,8);、
(2)当x=2时,y=-![]() x+3=2,
x+3=2,
∴点D的坐标为(2,2),
过点D作DE⊥BC,垂足为点E,设抛物线对称轴与x轴的交点为点F,如图1所示.
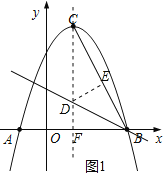
∵抛物线的顶点坐标为(2,8),
∴点F的坐标为(2,0),
∵点B的坐标为(6,0),
∴CF=8,CD=6,DF=2,BF=4,BC=![]() =4
=4![]() ,BD=
,BD=![]() =2
=2![]() ,
,
∴sin∠BCF=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DE=![]() ,
,
∴BE=![]() =
=![]() ,
,
∴cot∠CBD=![]() =
=![]() =
=![]() ;
;
(3)设直线PB与y轴交于点M,如图2所示.
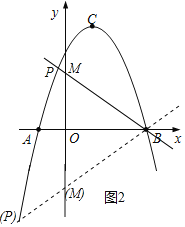
∵∠PBA=∠CBD,
∴cot∠PBA=![]() ,即
,即![]() ,
,
∴OM=![]() ,
,
∴点M的坐标为(0,![]() )或(0,-
)或(0,-![]() ),
),
设直线BP的解析式为y=mx+n(m≠0),
将B(6,0),M(0,![]() )代入y=mx+n,得:
)代入y=mx+n,得: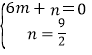 ,
,
解得: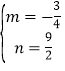 ,
,
∴直线BP的解析式为y=-![]() x+
x+![]() ,
,
同理,当点M的坐标为(0,-![]() )时,直线BP的解析式为y=-
)时,直线BP的解析式为y=-![]() x+
x+![]() ,
,
联立直线BP与抛物线的解析式成方程组,得: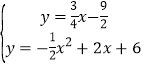 或
或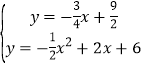 ,
,
解得: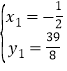 ,
,![]() 或
或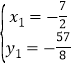 ,
,![]() ,
,
∴点P的坐标为(-![]() ,
,![]() )或(-
)或(-![]() ,-
,-![]() ).
).

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?