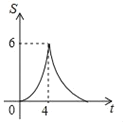
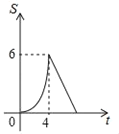
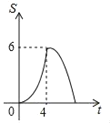
��Ŀ����
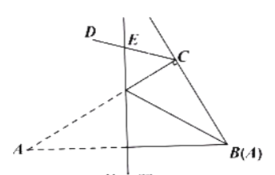
����Ŀ�� ��֪������y=![]() x2+bx+c������A��-2��0����B��0��-4����x�ύ����һ��C������BC��
x2+bx+c������A��-2��0����B��0��-4����x�ύ����һ��C������BC��

��1���������ߵĽ���ʽ��
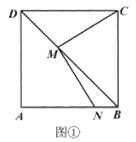
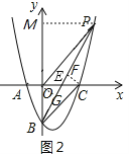
��2����ͼ��P�ǵ�һ��������������һ�㣬BP��x���ڵ�E����S��PBO=S��PBC����֤��E��OC���е㣻
��3���ڣ�2�������������P�����꣮
��4���ڣ�2�����������������Ƿ���ڵ�D��ʹ��ACD���������ABP�������ȣ������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2-x-4����2������������3��P��6��8������4�����ڣ�D������Ϊ��6��8����-4��8��
x2-x-4����2������������3��P��6��8������4�����ڣ�D������Ϊ��6��8����-4��8��
��������
��1�����ô���ϵ�����������ߵĽ���ʽ��
��2����y=0����������x��Ľ���C�����꣬����POB����PBC�ĸ��ߣ����������ȿɵ�OG=CF��֤����OEG�ա�CEF����OE=CE����E��OC���е㣻
��3���ɵ�OE=CE=2���������Ǻ�����ʽ�ɵ�P�����ꣻ
��4������S��ABP=S��AEP+S��AEB�������ABP��������������ȿ������D�������꣬���������߽���ʽ�ɵ�D������꣮
�⣺��1���ѵ�A��-2��0����B��0��-4������������y=![]() x2+bx+c�еã�
x2+bx+c�еã�
![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪy=![]() x2-x-4��
x2-x-4��
��2����y=0ʱ��![]() x2-x-4=0��
x2-x-4=0��
��ã�x=-2��4��
��C��4��0����
��ͼ1����O��OG��BP��G����C��CF��BP��F��
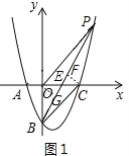
��S��PBO=S��PBC��
��![]() ��
��
��OG=CF��
�ߡ�OEG=��CEF����OGE��CFE��
���OEG�ա�CEF��AAS����
��OE=CE��
��E��OC���е㣻
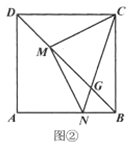
��3����P��x��![]() x2-x-4������ͼ2����P��PM��y����M��
x2-x-4������ͼ2����P��PM��y����M��
tan![]() =
=![]() ��
��
��BM=2PM��
��4+![]() x2-x-4=2x��
x2-x-4=2x��
x2-6x=0��
x1=0���ᣩ��x2=6��
��P��6��8����
��4����OE=2��OA=2��
��AE=OA+OE=4��
��S��ABP=S��AEP+S��AEB=![]() =24��
=24��
��AC=6����ACD��������ABP�������ȣ�
��![]() ��
��
��|yD|=8��
��yD=��8��
��![]() ʱ��
ʱ��
���x1=6��x2=-4��
��D1��6��8����D2��-4��8����
��![]() ʱ������û��ʵ������
ʱ������û��ʵ������
�ۺϿɵ�D������Ϊ��6��8����-4��8����