题目内容
【题目】如图,抛物线y=ax2 +bx+ 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
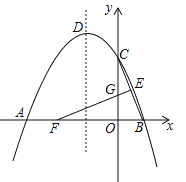
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
【答案】(1)![]() 顶点D的坐标为(-1,
顶点D的坐标为(-1,![]() )
)
(2)H(![]() ,
,![]() )
)
(3)K(-![]() ,
,![]() )
)
【解析】
(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值,进而可用配方法求出其顶点D的坐标;
(2)根据抛物线的解析式可求出C点的坐标,由于CD是定长,若△CDH的周长最小,那么CH+DH的值最小,由于EF垂直平分线段BC,那么B、C关于直线EF对称,所以BD与EF的交点即为所求的H点;易求得直线BC的解析式,关键是求出直线EF的解析式;由于E是BC的中点,根据B、C的坐标即可求出E点的坐标;可证△CEG∽△COB,根据相似三角形所得的比例线段即可求出CG、OG的长,由此可求出G点坐标,进而可用待定系数法求出直线EF的解析式,由此得解;
(3)过K作x轴的垂线,交直线EF于N;设出K点的横坐标,根据抛物线和直线EF的解析式,即可表示出K、N的纵坐标,也就能得到KN的长,以KN为底,F、E横坐标差的绝对值为高,可求出△KEF的面积,由此可得到关于△KEF的面积与K点横坐标的函数关系式,根据所得函数的性质即可求出其面积的最大值及对应的K点坐标.
(1)由题意,得![]() 解得
解得![]() ,b=-1.
,b=-1.
所以抛物线的解析式为![]() ,顶点D的坐标为(-1,
,顶点D的坐标为(-1,![]() ).
).
(2)设抛物线的对称轴与x轴交于点M.因为EF垂直平分BC,即C关于直线EG的对称点为B,连结BD交于EF于一点,则这一点为所求点H,使DH+CH最小,即最小为
DH+CH=DH+HB=BD=![]() .而
.而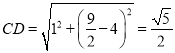 .
.
∴△CDH的周长最小值为CD+DR+CH=![]() .
.
设直线BD的解析式为y=k1x+b,则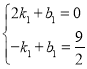 解得
解得![]() ,b1= 3.
,b1= 3.
所以直线BD的解析式为y=![]() x+ 3.
x+ 3.
由于BC= 2![]() ,CE=BC∕2 =
,CE=BC∕2 =![]() ,Rt△CEG∽△COB,
,Rt△CEG∽△COB,
得CE:CO=CG:CB,所以CG= 2.5,GO= 1.5.G(0,1.5).
同理可求得直线EF的解析式为y=![]() x+
x+![]() .
.
联立直线BD与EF的方程,解得使△CDH的周长最小的点H(![]() ,
,![]() ).
).
(3)设K(t,![]() ),xF<t<xE.过K作x轴的垂线交EF于N.
),xF<t<xE.过K作x轴的垂线交EF于N.
则KN=yK-yN=![]() -(
-(![]() t+
t+![]() )=
)=![]() .
.
所以S△EFK=S△KFN+S△KNE=![]() KN(t+ 3)+
KN(t+ 3)+![]() KN(1-t)= 2KN= -t2-3t+ 5 =-(t+
KN(1-t)= 2KN= -t2-3t+ 5 =-(t+![]() )2+
)2+![]() .
.
即当t=-![]() 时,△EFK的面积最大,最大面积为
时,△EFK的面积最大,最大面积为![]() ,此时K(-
,此时K(-![]() ,
,![]() ).
).

 步步高达标卷系列答案
步步高达标卷系列答案