题目内容
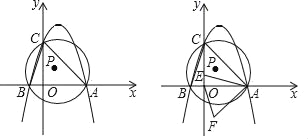
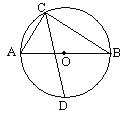
【题目】如图,⊙O的直径AB的长为10,弦AC长为6,∠ACB的平分线交⊙O于D,则CD长为( )
A. 7 B. ![]() C.
C. ![]() D. 9
D. 9
【答案】B
【解析】
作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,△CDF≌△CDG,得出CF=7,又△CDF是等腰直角三角形,从而求出CD=![]() .
.
解答:解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.

∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,弧AD=弧BD,
∴DA=DB.
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG.
∵AC=6,BC=8,
∴AF=1,(也可以:设AF=BG=X,BC=8,AC=6,得8-x=6+x,解x=1)
∴CF=7,
∵△CDF是等腰直角三角形,(这里由CFDG是正方形也可得).
∴CD=![]() .
.
故选B.

练习册系列答案
相关题目