题目内容
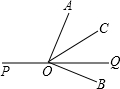如图所示，O是直线PQ上一点，∠AOB是直角，OC平分∠AOQ，∠BOQ=20°，求∠POC的度数．分析：求出∠AOQ，求出∠COQ，代入∠PCO=180°-∠COQ求出即可．
解答：解：∵∠AOB是直角，∠BOQ=20°，
∴∠AOQ=90°-20°=70°，
∵OC平分∠AOQ，
∴∠COQ=
∠AOQ=35°，
∴∠POC=180°-∠COQ=180°-35°=145°．
∴∠AOQ=90°-20°=70°，
∵OC平分∠AOQ，
∴∠COQ=
| 1 |
| 2 |
∴∠POC=180°-∠COQ=180°-35°=145°．
点评：本题考查了邻补角，角平分线定义的应用，主要考查学生的计算能力．
练习册系列答案
相关题目
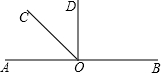如图所示，O是直线AB上一点，∠AOC=
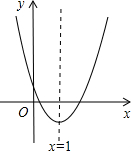（2013•广安）已知二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=1．下列结论：
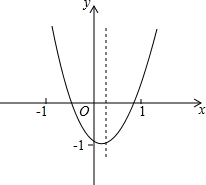已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，对称轴是直线
0°．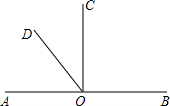
如图所示，0是直线AB上一点，0C是∠AOB的平分线．