题目内容
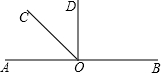 如图所示,O是直线AB上一点,∠AOC=
如图所示,O是直线AB上一点,∠AOC=| 1 | 3 |
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
分析:利用∠AOC=
∠BOC及补角的性质就可求出∠COD的度数;求出∠AOD的度数就可知道OD与AB的位置关系.
| 1 |
| 3 |
解答:解:(1)∵∠AOC+∠BOC=180°,∠AOC=
∠BOC,
∴
∠BOC+∠BOC=180°,
解得∠BOC=135°,
∴∠AOC=180°-∠BOC
=180°-135°=45°,
∵OC平分∠AOD,
∴∠COD=∠AOC=45°.
(2)OD⊥AB.
理由:由(1)知
∠AOC=∠COD=45°,
∴∠AOD=∠AOC+∠COD=90°,
∴OD⊥AB(垂直定义).
| 1 |
| 3 |
∴
| 1 |
| 3 |
解得∠BOC=135°,
∴∠AOC=180°-∠BOC
=180°-135°=45°,
∵OC平分∠AOD,
∴∠COD=∠AOC=45°.
(2)OD⊥AB.
理由:由(1)知
∠AOC=∠COD=45°,
∴∠AOD=∠AOC+∠COD=90°,
∴OD⊥AB(垂直定义).
点评:此题主要考查了补角的性质及垂直的定义,要注意领会由直角得垂直这一要点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
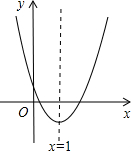 (2013•广安)已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:
(2013•广安)已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论: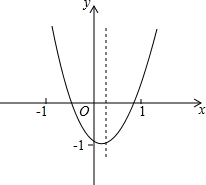 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线 0°.
0°.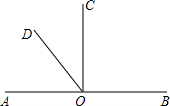 如图所示,0是直线AB上一点,0C是∠AOB的平分线.
如图所示,0是直线AB上一点,0C是∠AOB的平分线.