题目内容
如图所示，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，∠BOE=
∠EOC，∠DOE=6
0°．
（Ⅰ）求∠EOC的度数；
（Ⅱ）在上图中，哪些角互为余角？为什么？互为补角的角有几对？
| 1 | 3 |
0°．（Ⅰ）求∠EOC的度数；
（Ⅱ）在上图中，哪些角互为余角？为什么？互为补角的角有几对？
分析：（1）可以设∠BOE为x°，就可以根据条件列方程解决，求出∠BOE，继而求出∠EOC的度数；
（2）根据余角和补角的概念求解即可．
（2）根据余角和补角的概念求解即可．
解答：解：（1）设∠BOE为x°，则∠DOB=60°-x°，
由OD平分∠AOB，
得∠AOB=2∠DOB，
故有3x+x+2（60-x）=180，
解方程得x=30，
故∠EOC=90°．
（2）∵∠AOD，∠BOD和∠BOE都等于30°，∠DOE和∠AOB都等于60°，
∴互为余角的角有：∠AOD和∠DOE，∠AOD和∠AOB，
∠BOD和∠DOE，∠BOD和∠AOB，
∠BOE和∠DOE，∠BOE和∠AOB．
互为补角的角有6对．
由OD平分∠AOB，
得∠AOB=2∠DOB，
故有3x+x+2（60-x）=180，
解方程得x=30，
故∠EOC=90°．
（2）∵∠AOD，∠BOD和∠BOE都等于30°，∠DOE和∠AOB都等于60°，
∴互为余角的角有：∠AOD和∠DOE，∠AOD和∠AOB，
∠BOD和∠DOE，∠BOD和∠AOB，
∠BOE和∠DOE，∠BOE和∠AOB．
互为补角的角有6对．
点评：考查了根据角平分线的性质和已知条件列方程求解，难度适中，方程思想是解决问题的基本思考方法．
练习册系列答案
相关题目
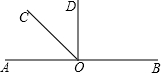如图所示，O是直线AB上一点，∠AOC=
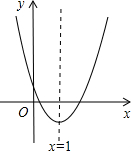（2013•广安）已知二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=1．下列结论：
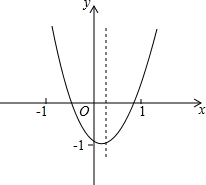已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，对称轴是直线
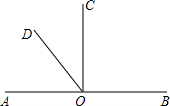如图所示，0是直线AB上一点，0C是∠AOB的平分线．