Question

【题目】如图，直线l：y＝x，点A1坐标为（1，0），过点A1作x轴的垂线交直线l于点B1，以原点O为圆心，OB1为半径画弧交x轴于点A2；再过点A2作x的垂线交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3，…，按此做法进行下去．

求：（1）点B1的坐标和∠A1OB1的度数；

（2）弦A4B3的弦心距的长度．

Answer 1

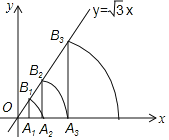
【答案】（1）∠A1OB1＝60°，B1（1，）；（2）4．

【解析】

（1）求出tan∠A1OB1的值，A1B1即可解决问题．

（2）连接A4B3，作OH⊥A4B3于H．求出OH即可．

（1）∵直线的解析式y＝x，

∴tan∠A1OB1＝＝，

∴∠A1OB1＝60°，OA1＝1，

∴A1B1＝，OA2＝OB1＝2，

∴B1（1，）．

（2）连接A4B3，作OH⊥A4B3于H．

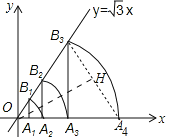
由题意OA1＝1，OA2＝2，OA3＝4，OA4＝8，

∵OA4＝OB3，OH⊥A4B3，

∴∠A4OH＝∠A4OB3＝30°，

∴OH＝OA4cos30°＝8×＝4．