题目内容
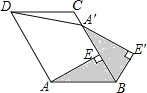
【题目】如图,已知平行四边形ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的度数为 .
【答案】160°.
【解析】
试题分析:根据平行四边形的性质得∠ABC=∠ADC=60°,AD∥BC,则根据平行线的性质可计算出∠DA′B=130°,接着利用互余计算出∠BAE=30°,然后根据旋转的性质得∠BA′E′=∠BAE=30°,于是可得∠DA′E′=160°.
解:∵四边形ABCD为平行四边形,
∴∠ABC=∠ADC=60°,AD∥BC,
∴∠ADA′+∠DA′B=180°,
∴∠DA′B=180°﹣50°=130°,
∵AE⊥BE,
∴∠BAE=30°,
∵△BAE顺时针旋转,得到△BA′E′,
∴∠BA′E′=∠BAE=30°,
∴∠DA′E′=130°+30°=160°.
故答案为160°.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目