题目内容
【题目】已知点A(s,t)在反比例函数![]() (k为常数,k≠0)的图象上.
(k为常数,k≠0)的图象上.
(1)当s=﹣1,t=3时,则k= ;
(2)当点A在第二象限时,将双曲线![]() (x<0)沿着y轴翻折,翻折后的曲线与原曲线记为曲线L,与过A点的直线y=b(b>0)交于点C,连接AO,过点O作AO的垂线与直线y=b交于点B.
(x<0)沿着y轴翻折,翻折后的曲线与原曲线记为曲线L,与过A点的直线y=b(b>0)交于点C,连接AO,过点O作AO的垂线与直线y=b交于点B.
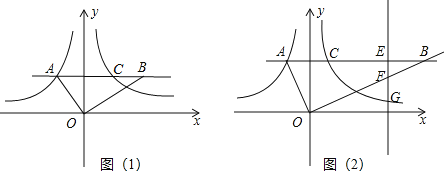
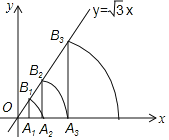
①如图(1),当![]() 时,求
时,求![]() 值;
值;
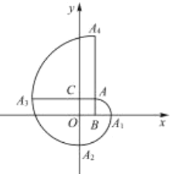
②如图(2),若A(﹣1,![]() ),作直线x=n(n>0)交曲线L于G点,分别交射线AB,射线OB于点E,F,当
),作直线x=n(n>0)交曲线L于G点,分别交射线AB,射线OB于点E,F,当![]() 时,直接写出n的取值范围.
时,直接写出n的取值范围.
【答案】(1)-3;(2)①![]() ;②0<n<3﹣
;②0<n<3﹣![]() 或1+
或1+![]() <n<3+
<n<3+![]() .
.
【解析】
(1)将点A坐标代入解析式可求k;
(2)①设直线y=b与y轴交于点D,由题意可证△AOD∽△OBD,可得![]() ,即可求解;
,即可求解;
②分当0<n<1时,当1<n<![]() 时,当
时,当![]() <n<3时,当n>3时,四种情况讨论即可.
<n<3时,当n>3时,四种情况讨论即可.
解:(1)∵点A(s,t)在反比例函数![]() 的图象上,且s=﹣1,t=3,
的图象上,且s=﹣1,t=3,
∴k=st=﹣3
故答案为﹣3.
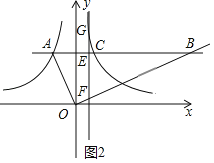
(2)①如图,设直线y=b与y轴交于点D,

∵点A与点C关于y轴对称,
∴C(﹣s,t),AD=CD=﹣s,OD=t.
∵OA⊥OB,
∴∠AOB=∠ADO=∠ODB=90°,
∴∠OAD+∠OBD=∠OAD+∠AOD=90°,
∴∠AOD=∠OBD,
∴△AOD∽△OBD,
∴![]() ,
,
∴BD=![]() ,
,
∴BC=BD﹣CD=![]() ,
,
∵![]() ,即3AC=2BC,
,即3AC=2BC,
∴3(﹣2s)=2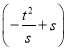 ,
,
整理得:t2=4s2,即|t|=2|s|,
∵点A在第二象限,s<0,t>0,
∴![]() ;
;
②∵A(﹣1,![]() ),由①得xB=﹣
),由①得xB=﹣![]() ,
,
∴C(1,![]() ),B(3,
),B(3,![]() ),
),
∴直线OB解析式为:y=![]() x,曲线L在x>时解析式为:y=
x,曲线L在x>时解析式为:y=![]() ,
,
∴直线OB与曲线L在第一象限交点为(![]() ,1),
,1),
∵直线x=n(n>0)交曲线L于G点,交射线AB于点E,交射线OB于点F,
∴G(n,![]() ),E(n,
),E(n,![]() ),F(n,
),F(n,![]() );
);
i)如图2,当0<n<1时,EF=![]() ,FG=
,FG=![]() ,
,
![]() ,即
,即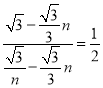 ,解得:n1=3+
,解得:n1=3+![]() (舍去),n2=3﹣
(舍去),n2=3﹣![]() ;
;
ii)如图3,当1<n<![]() 时,EF>FG,不合题意;
时,EF>FG,不合题意;
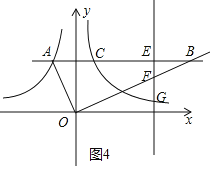
iii)如图4,当![]() <n<3时,EF=
<n<3时,EF=![]() ,FG=
,FG=![]() ,
,
![]() ,即
,即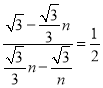 ,解得:n1=1+
,解得:n1=1+![]() ,n2=1﹣
,n2=1﹣![]() (舍去);
(舍去);
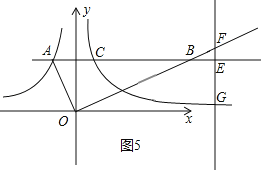
iiii)如图5,当n>3时,EF=![]() ,FG=
,FG=![]() ,
,
![]() ,即
,即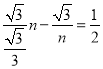 ,解得:n1=3+
,解得:n1=3+![]() ,n2=3﹣
,n2=3﹣![]() (舍去),
(舍去),
综上所述,当![]() 时,0<n<3﹣
时,0<n<3﹣![]() 或1+
或1+![]() <n<3+
<n<3+![]() .
.


【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小彤根据学习函数的经验,对函数y=
的图象与性质.小彤根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
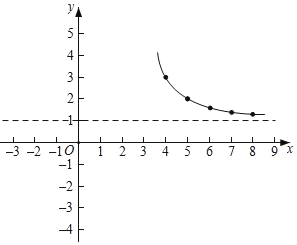
(4)观察图象,写出该函数的一条性质 ;
(5)若函数y=![]() 的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
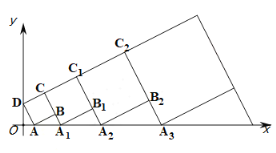
【题目】在平面直角坐标系![]() 中,正方形ABCD的位置如图所示,点
中,正方形ABCD的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,…按这样的规律进行下去,第
,…按这样的规律进行下去,第![]() 个正方形的面积为_____________.
个正方形的面积为_____________.
【题目】为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C
(1)小明将垃圾分装在三个袋中,任意投放,用画树状图或列表的方法求把三个袋子都放错位置的概率是多少?
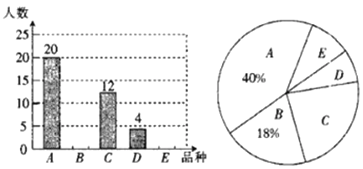
(2)某学习小组为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如表(单位:吨):
A | B | C | |
a | 40 | 10 | 10 |
b | 3 | 24 | 3 |
c | 2 | 2 | 6 |
调查发现,在“可回收垃圾”中塑料类垃圾占10%,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生200吨生活垃圾假设该城市每天处理投放正确的垃圾,每天大概可回收多少吨塑料类垃圾的二级原料?