题目内容
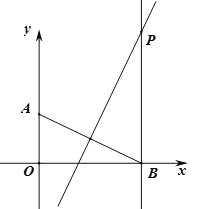
【题目】在平面直角坐标系中,△AOB的位置如图所示,∠AOB=90°,AO=BO,点A的坐标为(-1, 2) .抛物线y = ax2 + bx (a≠0)恰好经过A, B两点.
(1)直接写出点B坐标 .
(2)求该抛物线的函数表达式.
(3)设A关于抛物线的对称轴l的对称点为A',求△AA' B的面积.
【答案】(1)点B坐标 (2,1);(2)y=![]() ;(3)
;(3)![]()
【解析】
(1)过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,证明△OAC≌△BOD,得到OC=BD=1,AC=OD=2即可解决问题;
(2)根据A,B的坐标,利用待定系数法求抛物线的解析式即可;
(3)求出抛物线的对称轴,然后可得点A’的坐标,根据三角形面积公式计算即可.
解:(1)过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
∵∠AOB=∠ACO=∠ODB=90°,
∴∠BOD=90°-∠AOC=∠OAC,
在△OAC和△BOD中,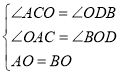 ,
,
∴△OAC≌△BOD,
∴OC=BD,AC=OD,
∵A(-1,2),
∴OC=BD=1,AC=OD=2,
∴点B坐标为 (2,1) ;

(2) 把 A(-1,2),B(2,1)代入![]() 得,
得,![]() ,
,
解得: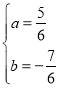 ,
,
∴该抛物线的函数表达式为:![]() ;
;
(3)∵抛物线对称轴为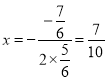 ,A(-1,2),
,A(-1,2),
∴A’坐标为(![]() ,2),
,2),
∴![]() ,
,
∴S△AA’B=![]() AA’×∣yA-yB∣
AA’×∣yA-yB∣![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小彤根据学习函数的经验,对函数y=
的图象与性质.小彤根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
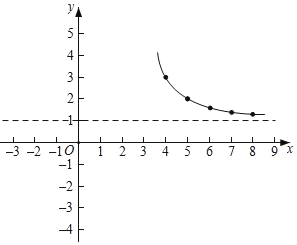
(4)观察图象,写出该函数的一条性质 ;
(5)若函数y=![]() 的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;