题目内容
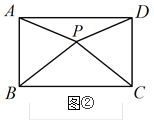
【题目】如图,矩形![]() 中,
中,![]() cm,
cm,![]() cm,动点
cm,动点![]() 以2cm╱s的速度从点
以2cm╱s的速度从点![]() 开始沿折线
开始沿折线![]() —
—![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 以2cm╱s的速度从点D开始沿折线
以2cm╱s的速度从点D开始沿折线![]() —
—![]() 向点终点
向点终点![]() 运动.如果点
运动.如果点![]() ,
,![]() 同时出发,设点
同时出发,设点![]() 运动的时间为t秒.
运动的时间为t秒.
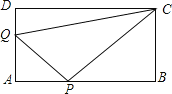
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求△CPQ的面积(可用含有t的代数式表示).
【答案】(1)![]() ;(2)①0≤x≤3,s=36-12t+2t2;3<x≤6,s=18;6<x≤9,s=2t2-36t+162
;(2)①0≤x≤3,s=36-12t+2t2;3<x≤6,s=18;6<x≤9,s=2t2-36t+162
【解析】
(1)用含t的式子表示AQ,AP,根据等腰直角三角形的性质即可求解;
(2)根据题意分①Q在线段AD上,P在线段AB上,②Q,P都在线段AB上,③Q在线段AB上,P在线段BC上依次求解即可.
(1)∵矩形![]() 中,
中,![]() cm,
cm,![]() cm,
cm,
∴AD=6cm,CD=12cm,
依题意得AQ=6-2t,AP=2t,
∵△QAP为等腰直角三角形
∴AQ= AP,即6-2t=2t,
解得![]()
故![]() 时,△QAP为等腰直角三角形
时,△QAP为等腰直角三角形
(2)当①Q在线段AD上,P在线段AB上,
即0≤t≤3时,DQ=2t,AQ=6-2t,AP=2t,BP=12-2t,
∴S△CPQ=S四边形ABCD-S△CDQ-S△APQ-S△BCP
=AB×BC-![]() ×CD×DQ-
×CD×DQ-![]() ×AP×AQ-
×AP×AQ-![]() ×BP×BC
×BP×BC
= 12×6-![]() ×12×2t-
×12×2t-![]() ×2t×(6-2t)-
×2t×(6-2t)-![]() ×(12-2t)×6
×(12-2t)×6
=36-12t+2t2
②Q,P都在线段AB上,即3<t≤6时,
AQ=2t-6,AP=2t,
∴PQ= AP-AQ=6,
S△CPQ=![]() ×QP×BC=
×QP×BC=![]() ×6×6=18;
×6×6=18;
③Q在线段AB上,P在线段BC上,即6<t≤9时,
AQ=2t-6,BQ=AB-AQ=18-2t,BP=2t-12,CP=BC-BP=18-2t,
∴S△CPQ=![]() ×CP×BQ=
×CP×BQ=![]() ×(18-2t)×(18-2t)= 2t2-36t+162
×(18-2t)×(18-2t)= 2t2-36t+162
故0≤t≤3,s=36-12t+2t2;
3<t≤6,s=18;
6<t≤9,s=2t2-36t+162.