题目内容
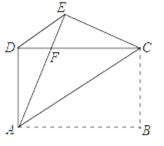
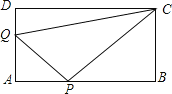
【题目】如图所示,四边形ABCD是矩形,已知PB=PC.
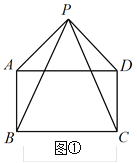
(1)若P是矩形外一点,求证:PA=PD;
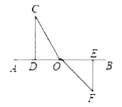
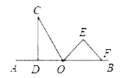
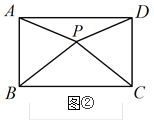
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
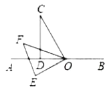
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
【答案】(1)详见解析;(2)=;(3)成立,理由详见解析.
【解析】
(1)由四边形ABCD是矩形,可得AB=DC,∠ABC=∠DCB=90°,又由PB=PC可得∠PBC=∠PCB,求出∠PBA=∠PCD,进而利用SAS证明△APB≌△DPC即可得到PA=PD;
(2)当P是矩形边AD(或BC)上的一点,通过HL可证Rt△APB≌Rt△DPC,得到PA=PD;
(3)当点P在矩形ABCD内部时,同(1)可证△APB≌△DPC,得到PA=PD.
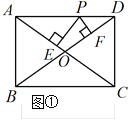
(1)证明:如图①,

∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,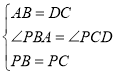 ,
,
∴△APB≌△DPC,
∴PA=PD;
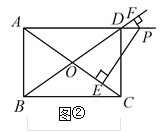
(2) 如图②,当P是矩形边AD上的一点,
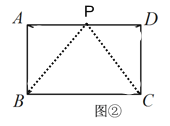
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,PB=PC,
∴Rt△APB≌Rt△DPC(HL),
∴PA=PD,
当P是矩形边BC上的一点,同理可得:PA=PD,
∴若P是矩形边AD(或BC)上的一点,则PA=PD;
(3)成立.
理由如下:
如图③,
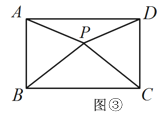
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,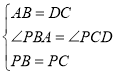 ,
,
∴△APB≌△DPC,
∴PA=PD.

练习册系列答案
相关题目