Question

【题目】如图①，A，B，C，D四点共圆，过点C的切线CE∥BD，与AB的延长线交于点E．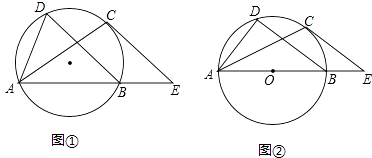

（1）求证：∠BAC=∠CAD；
（2）如图②，若AB为⊙O的直径，AD=6，AB=10，求CE的长；
（3）在（2）的条件下，连接BC，求 的值．

Answer 1

【答案】
（1）证明：连结OC，如图①，

∵CE为切线，

∴OC⊥CE，

∵CE∥BD，

∴OC⊥BD，

∴ ，

∴∠BAC=∠CAD；

（2）解：如图②，连结OC交BD于E，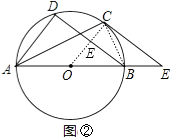

由（1）得OC⊥BD，则BE=DE，

∵AB为直径，

∴∠D=90°，

∴BD= =8，

∴BE= BD=4，

在Rt△OBE中，OE= =3，

∵BE∥CE，

∴△OBE∽△OCE，

∴ ，即 ，

∴CE= ；

（3）解：∵OE=3，OC=5，

∴CE=5﹣3=2，

∵ ，

∴∠CDB=∠CAB，

∵tan∠CBE= = ，

∴tan∠CAB=tan∠CBE= ，

∵tan∠CAB= ，

∴ = ．

【解析】（1）根据切线的性质和已知条件，得到OC⊥BD，根据垂径定理得到两弧相等，根据在同圆中相等的弧所对的圆周角相等，得到∠BAC=∠CAD；（2）由（1）知OC⊥BD，BE=DE；AB为直径，得到∠D=90°，根据勾股定理求出BD、BE、OE的长，由BE∥CE，得到△OBE∽△OCE，得到比例，求出CE的值；（3）根据在同圆中相等的弧所对的圆周角相等，得到∠CDB=∠CAB，由三角函数tan∠CBE的值，求出tan∠CAB=tan∠CBE的值，求出的值.
【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)，还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键．