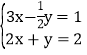题目内容
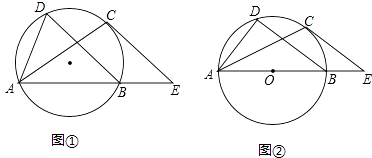
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1
B.1≤r≤ ![]()
C.1≤r≤ ![]()
D.1≤r≤4
【答案】C
【解析】解:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连接OA、OB,如图所示
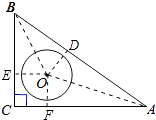
则四边形OECF是正方形,
∴OF=CF=OE=CE,
∵∠C=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵O是△ABC的内心,
∴CE=CF=OF=OE= ![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∴AF=AC﹣CF=3,BE=BC﹣CE=2,
∴OA= ![]() ,OB=
,OB= ![]() =
= ![]() ,
,
当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当1<r≤ ![]() 时,以O为圆心,r为半径的圆与线段AB有两个交点;
时,以O为圆心,r为半径的圆与线段AB有两个交点;
当 ![]() <r≤
<r≤ ![]() 时,以O为圆心,r为半径的圆与线段AB有1个交点;
时,以O为圆心,r为半径的圆与线段AB有1个交点;
∴以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是1≤r≤ ![]() ;
;
所以答案是:C
【考点精析】掌握直线与圆的三种位置关系和三角形的内切圆与内心是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 ![]() 时,
时, ![]() ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是(填正确结论的序号).