题目内容
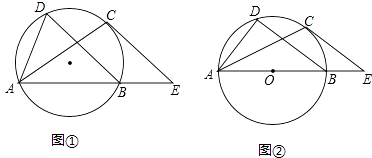
【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3 . C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
【答案】
(1)解:顶点C为(﹣1,﹣4).
∵点B(1,0)在抛物线C1上,∴0=a(1+1)2﹣4,解得,a=1;
(2)解:①∵C2与C1关于x轴对称,
∴抛物线C2的表达式为y=﹣(x+1)2+4,
抛物线C3由C2平移得到,
∴抛物线C3为y=﹣(x﹣3)2+4=﹣x2+6x﹣5,
∴E(5,0),
设直线CE的解析式为:y=kx+b,
则 ![]() ,
, 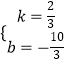 ,
,
∴直线CE的解析式为y= ![]() ,
,
设P(x,﹣x2+6x﹣5),则F(x, ![]() ),
),
∴PF=(﹣x2+6x﹣5)﹣( ![]() )=﹣x2+
)=﹣x2+ ![]() x﹣
x﹣ ![]() =﹣(x﹣
=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,PF有最大值为
时,PF有最大值为 ![]() ;
;
②若PE=EF,∵PF⊥x轴,
∴x轴平分PF,
∴﹣x2+6x﹣5=﹣ ![]() ,
,
解得x1= ![]() ,x2=5(舍去)
,x2=5(舍去)
∴P( ![]() ,
, ![]() ).
).
【解析】(1)由抛物线的顶点式得到顶点C的坐标;由点B(1,0)在抛物线上,求出a的值;(2)①由C2与C1关于x轴对称,得到抛物线C2的表达式,抛物线C3由C2平移得到,得到抛物线C3的解析式,得到E点的坐标,直线CE的解析式,求出PF的最大值;②若PE=EF,∵PF⊥x轴,得到x轴平分PF,求出P点的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.

 阶梯计算系列答案
阶梯计算系列答案【题目】一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上为合格.成绩达到9分为优秀.这次测验中甲乙两组学生成绩分布的条形统计图如下:
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.
【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中甲、乙两组学生人数都为6人,成绩如下(单位:分):
甲:7,9,10,8,5,9;
乙:9,6,8,10,7,8
(1)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | |
甲组 | 8 | 9 | ||
乙组 |
| 8 | 8 |
(2)甲组学生说他们的众数高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出一条支持乙组学生观点的理由. .