题目内容
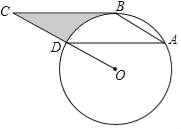
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)请探究线段AF与FG的倍数关系,并证明你的结论。
(3)设FG=x,△EFG的面积为y,求y关于x的函数解析式,并直接写出x的取值范围;
【答案】(1)见解析;(2)AF=3 FG ;(3)![]()
【解析】分析:(1)先证明∠A=∠2,然后利用相似三角形的判定方法即可得到结论;
(2)证明△EFG∽△AEG即可得解.
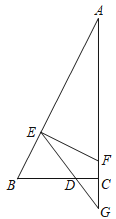
(3)作EH⊥AF于点H,如图1,利用勾股定理计算出AB=2![]() ,利用△EFG∽△AEG得到
,利用△EFG∽△AEG得到![]() ,再证明Rt△AEF∽Rt△ACB得到
,再证明Rt△AEF∽Rt△ACB得到![]() ,所以
,所以![]() ,则EG=2x,AG=4x,AF=3x,EF=
,则EG=2x,AG=4x,AF=3x,EF=![]() x,AE=
x,AE=![]() x,接着利用相似比表示出EH=
x,接着利用相似比表示出EH=![]() x,AH=
x,AH=![]() x,然后根据三角形面积公式表示出y与x的关系,最后利用CF=4-3x可确定x的范围;
x,然后根据三角形面积公式表示出y与x的关系,最后利用CF=4-3x可确定x的范围;
详解:(1)证明:∵ED=BD,
∴∠B=∠2,
∵∠ACB=90°,
∴∠B+∠A=90°.
∵EF⊥AB,
∴∠BEF=90°,
∴∠1+∠2=90°,
∴∠A=∠2,
∵∠EGF=∠AGE,
∴△EFG∽△AEG;
(2)答:AF=3 FG
证明:作EH⊥AF于点H.
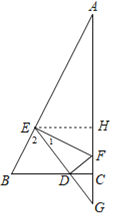
∵ 在Rt△ABC中,∠ACB=90°,BC=2,AC=4,
∴ ![]() .
.
∴ 在Rt△AEF中,∠AEF=90°,![]() .
.
∵ △EFG∽△AEG,
∴ ![]() .
.
∴ EG=2 FG,
∴AG=2 EG=4 FG
∴AF=3 FG
(3)∵ FG=x,
∴ EG=2x,AG=4x.
∴ AF=3x.
∵ EH⊥AF,
∴ ∠AHE=∠EHF=90°.
∴ ∠EFA+∠FEH=90°.
∵ ∠AEF=90°,
∴ ∠A+∠EFA=90°.
∴ ∠A=∠FEH.
∴ tanA =tan∠FEH.
∴ 在Rt△EHF中,∠EHF=90°,![]() .
.
∴ EH=2HF.
∵ 在Rt△AEH中,∠AHE=90°,![]() .
.
∴ AH=2EH.
∴ AH=4HF.
∴ AF=5HF.
∴ HF=![]() .
.
∴ ![]() .
.
∴ ![]() .
.
x的取值范围![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
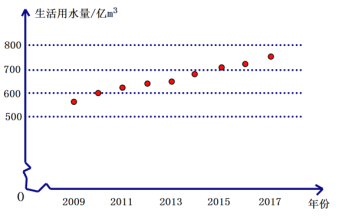
轻松课堂单元期中期末专题冲刺100分系列答案【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约![]() 亿
亿![]() (占总用水量的
(占总用水量的![]() ),工业用水量约为
),工业用水量约为![]() 亿
亿![]() ,生活用水量具体见下表.
,生活用水量具体见下表.
2019-2017年全国生活用水量表(单位:亿![]() )
)
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
用水量 |
|
|
|
|
|
|
|
|
|
(1)2017年全国总用水量约为 亿![]() ,其他用水约为 亿
,其他用水约为 亿![]() .
.
(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.