题目内容
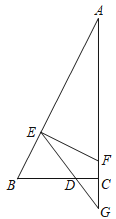
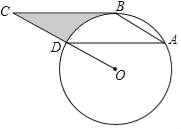
【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4![]() .
.
(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
【答案】(1)30°(2)![]()
【解析】分析:(1)连接OB,根据切线的性质求出∠OBC,根据三角形内角和定理求出∠BOC,根据圆周角定理推出即可;
(2)求出DM,解直角三角形求出OD,分别求出△OBC的面积和扇形DOB的面积,即可得出答案.
详解:(1)连接OB,交AD于M,
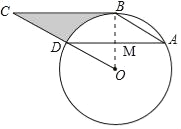
∵BC为⊙O切线,
∴∠OBC=90°,
∵∠C=30°,∠OBC=90°,
∴∠BOD=60°,
∴∠A=![]() ;
;
(2)∵AD∥BC,∠OBC=90°,
∴∠OMD=∠OBC=90°,
∴由垂径定理得DM=![]() ,
,
∵Rt△OMD中,DM=2![]() ,∠BOD=60°,
,∠BOD=60°,
∴OD=![]() ,
,
在Rt△OBC中,OB=4,∠BOC=60°,
∴BC=OB×tan∠BOC=4×tan60°=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴阴影部分的面积=![]() .
.

练习册系列答案
相关题目
【题目】某公司购进某种矿石原料300吨,用于生产甲、乙两种产品,生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
产品资源 | 甲 | 乙 |
矿石(吨) | 10 | 4 |
煤(吨) | 4 | 8 |
生产1吨甲产品所需成本费用为4000元,每吨售价4600元;
生产1吨乙产品所需成本费用为4500元,每吨售价5500元,
现将该矿石原料全部用完,设生产甲产品x吨,乙产品m吨,公司获得的总利润为y元.
(1)写出m与x之间的关系式
(2)写出y与x之间的函数表达式,并写出自变量的范围
(3)若用煤不超过200吨,生产甲产品多少吨时,公司获得的总利润最大,最大利润是多少?