Question

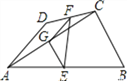
【题目】如图，四边形 ABCD 中，AD=BC，E、F、G 分别是 AB、CD、AC 的中点，若∠DAC=20 ，∠ACB=90 ，则 ∠FEG=( )

A. B. C. D.

Answer 1

【答案】A

【解析】分析：利用三角形的中位线定理可得EG、FG分别是△ABC和△ADC两个三角形的中位线，从而求出EG=FG，继而求得∠FGC和∠EGC的度数，再根据EG=FG，利用三角形内角和定理即可求出∠FEG的度数．

详解：

∵E、F、G分别是AB、CD、AC的中点，

∴EG、FG分别是△ABC和△ADC两个三角形的中位线，

∴EG∥BC，FG∥AD，且EG=FG=AD=，

∴∠FGC=∠DAC=20°，∠EGC=180°-∠ACB=90°，

∴∠EGF=∠FGC+∠EGC=110°，

又∵EG=FG，

∴∠FEG=（180°-∠EGF）=（180°-110°）=35°．

故选A．