题目内容
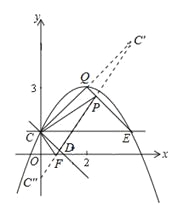
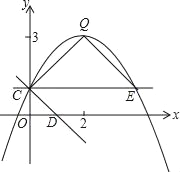
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
【答案】(1)y=﹣x+1;(2)y=![]() x2+2x+1;(3)证明见解析;(4)存在.为
x2+2x+1;(3)证明见解析;(4)存在.为![]() .
.
【解析】试题分析:(1)利用待定系数法求出直线解析式;
(2)利用待定系数法求出抛物线的解析式;
(3)关键是证明△CEQ与△CDO均为等腰直角三角形;
(4)如图所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小.如图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值.
(1)C(0,1),D(1,0)
∴直线CD的解析式为![]() ;
;
(2)设抛物线解析式为y=a(x-2)2+3,
易得y=![]() (x-2)2+3=
(x-2)2+3=![]() x2+2x+1
x2+2x+1
(3)OC=OD,OC⊥OD,∴△OCD为等腰直角三角形,
对称轴x=2与CE交于点M,M(2,1)
易知△QMC与△QME是等腰直角三角形
∴△ CQE也是等腰直角三角形
∴△CEQ∽△CDO
(4)存在。
如图作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称性得:
PC=PC′ CF=C″F
C,C′关于直线QE对称
C′(4,5)
又C″(-1,0) C′C″=![]()
∴△PCF的周长最小值是![]()