题目内容
【题目】如图所示,每个小正方形的边长为1cm
(1)求四边形ABCD的面积;
(2)四边形ABCD中有直角吗?若有,请说明理由.

【答案】(1)14![]() ;
;
(2)四边形ABCD中有直角.
【解析】
(1)根据四边形ABCD的面积=S矩形AEFH-S△AEB-S△BFC-S△CGD-S梯形AHGD即可得出结论;
(2)四边形ABCD中有直角.根据勾股定理得到BC=2![]() ,CD=
,CD=![]() ,BD=5,再根据勾股定理的逆定理即可求解.
,BD=5,再根据勾股定理的逆定理即可求解.
解:(1)如图,
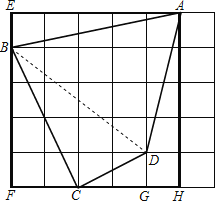
∵四边形ABCD的面积=S矩形AEFH-S△AEB-S△BFC-S△CGD-S梯形AHGD
=5×5-![]() ×1×5-
×1×5-![]() ×2×4-
×2×4-![]() ×1×2-
×1×2-![]() ×(1+5)×1
×(1+5)×1
=14![]() ;
;
(2)四边形ABCD中有直角.
理由:连结BD,由勾股定理得:
BC=2![]() ,CD=
,CD=![]() ,BD=5,
,BD=5,
∵BD2=BC2+CD2,
∴∠C=90°,
∴四边形ABCD中有直角.

【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?