题目内容
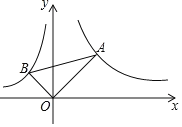
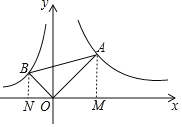
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=﹣
的图象经过点A,反比例函数y2=﹣![]() 的图象经过点B,则m的值是( )
的图象经过点B,则m的值是( )
A.m=3B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过A、B分别作AM⊥x轴,BN⊥x轴,垂足为M、N,首先证明△BON∽△OAM,根据三角函数和相似三角形的性质可得![]() ,然后设ON=a,BN=b,则MA=
,然后设ON=a,BN=b,则MA=![]() a,OM=
a,OM=![]() b,表示出点B和点A的坐标,根据反比例函数图象上点的坐标特征进而求出m的值.
b,表示出点B和点A的坐标,根据反比例函数图象上点的坐标特征进而求出m的值.
解:过A、B分别作AM⊥x轴,BN⊥x轴,垂足为M、N.
∵∠AOB=90°,∠AMO=∠BNO=90°,
∴∠BON+∠AOM=∠AOM+∠OAM=90°,
∴∠BON=∠OAM,
∴△BON∽△OAM,
∴![]() ,
,
∵∠OAB=30°,
∴tan30°=![]() =
=![]() ,
,
∴![]() ,
,
设ON=a,BN=b,则MA=![]() a,OM=
a,OM=![]() b,
b,
∴B(﹣a,b),A(![]() a,
a,![]() b).
b).
∵点B在反比例函数y2=﹣![]() 的图象上,
的图象上,
∴ab=1,
∵点A在反比例函数y1=![]() 的图象上,
的图象上,
∴m=![]() a
a![]() b=3ab=3,
b=3ab=3,
故选:A.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】阅读下面材料:
一般地,如果一个数列从第![]() 项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,它通常用字母
项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,它通常用字母![]() 表示,我们可以用公式
表示,我们可以用公式![]() 来计算等差数列的和.(公式中的n表示数的个数,a表示第一个数的值,)
来计算等差数列的和.(公式中的n表示数的个数,a表示第一个数的值,)
例如:3+5+7+9+11+13+15+17+19+21=10×3+![]() ×2=120.
×2=120.
用上面的知识解决下列问题.
(1)计算:2+8+14+20+26+32+38+44+50+56+62+68+74+80+86+92+98+104+110+116
(2)某县决定对坡荒地进行退耕还林.从2009年起在坡荒地上植树造林,以后每年植树后坡荒地的实际面积按一定规律减少,下表为2009、2010、2011、2012四年的坡荒地面积的统计数据.问到哪一年,可以将全县所有坡荒地全部种上树木.
2009年 | 2010年 | 2011年 | 2012年 | |
植树后坡荒地的实际面积(公顷) | 25 200 | 24 000 | 22 400 | 20400 |