题目内容
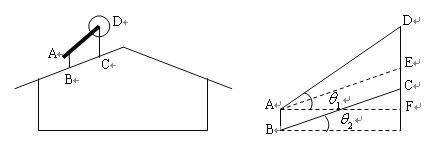
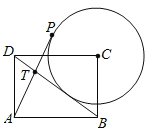
【题目】如图1,一根木棒AB,斜靠在与地面OM垂直的墙壁ON上,当木棒A端沿NO向下滑动时,同时B端沿射线OM向右滑动,实践发现木棒的中点P运动的路径是一个优美的几何图形,我们把这样的点叫优美点.如果木棒AB长为4,与地面的倾斜角∠ABO=60°.
(1)当木棒A端沿NO向下滑动到点O时,同时B端沿射线OM向右滑动到B′时,木棒的中点P所经过的路径长为多少?
(2)若点P为OB上由点O向点B运动的一运动点,连接AP.
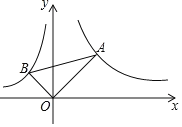
①如图2,设AP的中点为G,问点G是不是优美点,如是,请求出点P运动过程中G所经过的路径长.
②如图3,过点B作BR⊥AP,垂足为点R.点P运动过程中,点R是不是优美点,如是,请求出点R所经过的路径长.
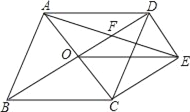
(3)如图4,若点P以每秒1个单位长度由点B向点O运动,同时点Q以每秒![]() 个单位长度的速度由点A向点O运动,连接PQ,S为PQ的中点,则在PQ的运动过程中,点S经过的路径长为多少?(直接写结果)
个单位长度的速度由点A向点O运动,连接PQ,S为PQ的中点,则在PQ的运动过程中,点S经过的路径长为多少?(直接写结果)

【答案】(1)![]() π;(2)①1,②
π;(2)①1,②![]() π;(3)2
π;(3)2
【解析】
(1)由题意OP=![]() AB=2,推出点P的运动轨迹是
AB=2,推出点P的运动轨迹是![]() ,利用弧长公式求解即可.
,利用弧长公式求解即可.
(2)①如图2中,取AO,AB的中点E,F,连接EF.点G是优美点,点P运动轨迹是△AOB的中位线EF.
②如图3中,点R是优美点,点R的运动轨迹是![]() ,圆心是AB的中点K,连接OK.
,圆心是AB的中点K,连接OK.
(3)首先证明PQ∥AB,推出PQ的中点S的运动轨迹是Rt△AOB的斜边AB上的中线OK.
解:(1)连接OP.
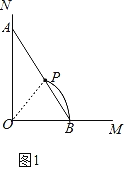
在Rt△AOB中,∵∠AOB=90°,AB=4,PA=PB,
∴OP=![]() AB=2,
AB=2,
∵OP=PB=2,∠ABO=60°,
∴△OPB是等边三角形,
∴∠POB=60°,
由题意点P的运动路径是![]() ,
,
∴点P的运动路径的长=![]() =
=![]() π.
π.
(2)①如图2中,取AO,AB的中点E,F,连接EF.
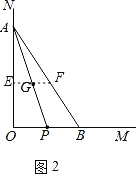
点G是优美点,点P运动轨迹是△AOB的中位线EF.
∵∠OAB=30°,∠AOB=90°,
∴OB=![]() AB=2,
AB=2,
∵AE=EO,AF=FB,
∴EF=![]() OB=1,
OB=1,
∴点P运动过程中G所经过的路径长为1.
②如图3中,点R是优美点,

∵AR⊥BR,
∴∠ARB=90°,
∴点R在AB为直径的圆上,点R的运动轨迹是![]() ,圆心是AB的中点K,连接OK.
,圆心是AB的中点K,连接OK.
∴点R所经过的路径长=![]() =
=![]() π.
π.
(3)
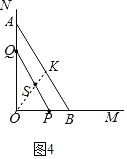
∵OA=![]() ,OB=2,AQ=
,OB=2,AQ=![]() t,BP=t,
t,BP=t,
∴![]()
∴PQ∥AB,
∴PQ的中点S的运动轨迹是Rt△AOB的斜边AB上的中线OK,
∴点S经过的路径长为![]() AB=2.
AB=2.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案