题目内容
【题目】问题探究,
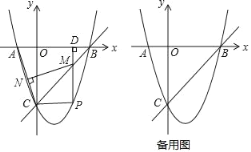
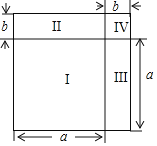
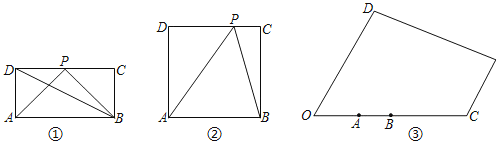
(1)如图①,在矩形ABCD中,AB=2AD,P为CD边上的中点,试比较∠APB和∠ADB的大小关系,并说明理由;
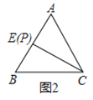
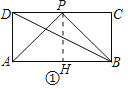
(2)如图②,在正方形ABCD中,P为CD上任意一点,试问当P点位于何处时∠APB最大?并说明理由;
问题解决
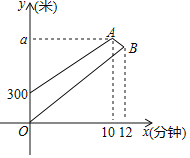
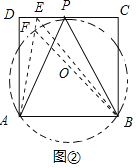
(3)某儿童游乐场的平面图如图③所示,场所工作人员想在OD边上点P处安装监控装置,用来监控OC边上的AB段,为了让监控效果最佳,必须要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
【答案】(1) 结论:∠APB>∠ADB ,理由见解析;(2) 当点P位于CD的中点时,∠APB最大,理由见解析;(3) 当经过A,B的⊙T与OD相切于P时,∠APB的值最大,理由见解析
【解析】
(1)作PH⊥AB于H,通过正方形和矩形的性质可得∠APB=90°,再根据∠ADB<90°,即可证明∠APB>∠ADB;
(2)假设P为CD的中点,如图②中,作△APB的外接圆⊙O,则此时CD切⊙O于点P,在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE,BF,根据∠AFB是△EFB的外角,可得∠AFB>∠AEB,再根据∠AFB=∠APB,从而可得∠APB>∠AEB,故点P位于CD的中点时,∠APB最大;
(3)作TH⊥OC于H,交OD于Q,连接TA,TB,OT.设TP=TA=TB=r,根据等边三角形的性质可得AH=HB=100![]() (m),再根据含30°角的直角三角形的性质可得AT=200
(m),再根据含30°角的直角三角形的性质可得AT=200![]() m,故AT=2AH,可得∠ATH=30°,即∠ATB=2∠ATH=60°,根据圆周角定理可得∠APB=
m,故AT=2AH,可得∠ATH=30°,即∠ATB=2∠ATH=60°,根据圆周角定理可得∠APB=![]() ∠ATB=30°,再根据含30°角的直角三角形的性质求出OQ和PQ的长度,再根据OP=OQ﹣PQ求解OP的长度即可.
∠ATB=30°,再根据含30°角的直角三角形的性质求出OQ和PQ的长度,再根据OP=OQ﹣PQ求解OP的长度即可.
解:(1)如图①中,结论:∠APB>∠ADB.
理由:作PH⊥AB于H.
∵四边形ABCD是矩形,PH⊥AB,
∴∠ADP=∠DAH=∠AHP=90°,
∴四边形ADPH是矩形,
∵AB=CD=2AD,DP=PC,
∴DA=DP,
∴四边形ADPH是正方形,
∴∠APH=45°,同理可证∠BPH=45°,
∴∠APB=90°,
∵∠ADB<90°,
∴∠APB>∠ADB.
(2)当点P位于CD的中点时,∠APB最大,理由如下:
假设P为CD的中点,如图②中,作△APB的外接圆⊙O,则此时CD切⊙O于点P,
在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE,BF,
∵∠AFB是△EFB的外角,
∴∠AFB>∠AEB,
∵∠AFB=∠APB,
∴∠APB>∠AEB,
故点P位于CD的中点时,∠APB最大.
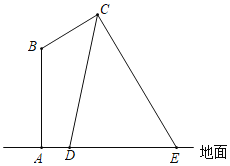
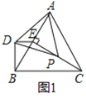
(3)如图③中,当经过A,B的⊙T与OD相切于P时,∠APB的值最大,
作TH⊥OC于H,交OD于Q,连接TA,TB,OT.设TP=TA=TB=r,
∵TA=TB,TH⊥AB,
∴AH=HB=100![]() (m),
(m),
∵∠OHQ=90°,∠O=60°,OH=OA+AH=(400+100![]() )(m),
)(m),
∴QH=![]() OH=(400
OH=(400![]() +300)(m),∠OQH=30°,
+300)(m),∠OQH=30°,
∴TQ=2PT=2r,
∵TH=![]() =
=![]() ,
,
∴2r+![]() =400
=400![]() +300,
+300,
整理得:3r2﹣(1600![]() +1200)r+60000+240000
+1200)r+60000+240000![]() =0,
=0,
∴(r﹣200![]() )(r﹣1000
)(r﹣1000![]() ﹣1200)=0,
﹣1200)=0,
∴r=200![]() 或1000
或1000![]() +1200(舍弃),
+1200(舍弃),
∴AT=200![]() m,
m,
∴AT=2AH,
∴∠ATH=30°,∠ATB=2∠ATH=60°,
∴∠APB=![]() ∠ATB=30°,
∠ATB=30°,
∴![]() ,
,![]()
∴OP=OQ﹣PQ=800+200![]() ﹣600=(200+200
﹣600=(200+200![]() )(m).
)(m).

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案