Question

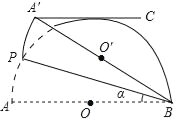
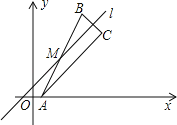
【题目】对于坐标平面内的点，先将该点向右平移1个单位，再向上平移2个单位，这种点的运动称为点的斜平移，如点P（2，3）经1次斜平移后的点的坐标为（3，5）．已知点A的坐标为（1，0）．如图，点M是直线l上的一点，点A关于点M的对称点为点B，点B关于直线l的对称点为点C．若点B由点A经n次斜平移后得到，且点C的坐标为（7，6），则点B的坐标为_____及n的值为______．

Answer 1

【答案】（5，8） 4

【解析】

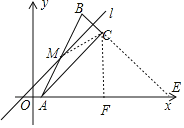
连接CM，根据中心对称可得：AM＝BM，由轴对称可得：MB＝MC，所以AM＝CM＝BM，进而可以证明△ABC是直角三角形，延长BC交x轴于点E，过点C作CF⊥AE于点F，可以证明△ACF是等腰直角三角形，可得E点坐标，进而可求直线BE的解析式，再根据点B由点A经n次斜平移得到，得点B（n+1，2n），代入直线解析式即可求得n的值，进而可得点B的坐标．

解：连接CM，

由中心对称可知：AM＝BM，

由轴对称可知：MB＝MC，

∴AM＝CM＝BM，

∴∠MAC＝∠ACM，∠MBC＝∠MCB，

∵∠MAC+∠ACM+∠MBC+∠MCB＝180°，

∴∠ACB＝90°，

∴△ABC是直角三角形．

延长BC交x轴于点E，过点C作CF⊥AE于点F，

∵A（1，0），C（7，6），

∴AF＝CF＝6，

∴△ACF是等腰直角三角形，

∵∠ACE＝90°，∴∠AEC＝45°，

∴E点坐标为（13，0），

设直线BE的解析式为y＝kx+b，

∵点C，E在直线上，

∴，

解得，

∴y＝﹣x+13，

∵点B由点A经n次斜平移得到，

∴点B（n+1，2n），

由2n＝﹣n﹣1，解得n＝4，

∴B（5，8）．

故答案为：（5，8）、4．