题目内容
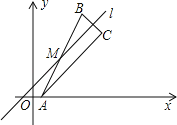
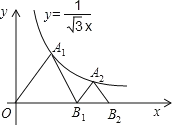
【题目】如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数![]() 的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
【答案】△OA1B1的面积=![]() ,△B1A2B2的面积=
,△B1A2B2的面积=![]() .
.
【解析】
分别过A1、A2作x轴的垂线,垂足分别为D、E,设OD=m,B1E=n(m>0,n>0).根据等边三角形的性质和含30度的直角三角形三边的关系得到A1的坐标为(m,![]() m),A2的坐标为(2m+n,
m),A2的坐标为(2m+n,![]() n),然后先后把A1、A2的坐标代入反比例解析式求得m、n的值,这样就确定两等边三角形的边长,然后根据等边三角形的面积公式计算即可.
n),然后先后把A1、A2的坐标代入反比例解析式求得m、n的值,这样就确定两等边三角形的边长,然后根据等边三角形的面积公式计算即可.
分别过A1、A2作x轴的垂线,垂足分别为D、E,如图,
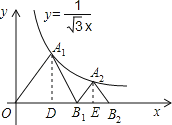
设OD=m,B1E=n(m>0,n>0).
∵△OA1B1,△B1A2B2是等边三角形,
∴∠OA1D=∠B1A2E=30°,
∴A1D=![]() OD=
OD=![]() m,A2E=
m,A2E=![]() B1E=
B1E=![]() n,OE=2m+n,
n,OE=2m+n,
∴A1的坐标为(m,![]() m),A2的坐标为(2m+n,
m),A2的坐标为(2m+n,![]() n),
n),
又∵点A1在函数![]() 的图象上,
的图象上,
∴![]() ,解得:
,解得:![]() (负值已舍),
(负值已舍),
∴A1的坐标为(![]() ,
,![]() ),
),
∴OB1=2m=![]() ,OE=
,OE=![]() +n.
+n.
∴A2的坐标为(![]() +n,
+n,![]() n),
n),
∵点A2在函数![]() 的图象上,
的图象上,
∴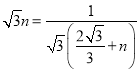 ,
,
整理得:![]() ,
,
解得:n1=![]() ,n2=
,n2=![]() (舍去),
(舍去),
∴n=![]() ,
,
∴A2的坐标为(![]() ,
,![]() ),
),
∴B1B2=2n=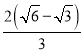 ,
,
∴△OA1B1的面积![]() ,
,
△B1A2B2的面积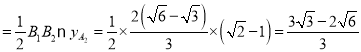 .
.

 名校课堂系列答案
名校课堂系列答案【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.