题目内容
【题目】如图![]() 是矩形
是矩形![]() 的对角线
的对角线![]() 分别是
分别是![]() 上的动点,
上的动点,![]() 则
则![]() 的最小值为____________
的最小值为____________

【答案】![]()
【解析】
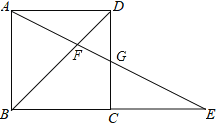
作点B关于AC的对称点B′,过点B′作B′E⊥BC于E,交AC于P,连接CB′交AD于F,连接BP,再根据矩形、轴对称、等腰三角形的性质得出FA=FC,那么在Rt△CDF中,运用勾股定理求出FC的长,然后由cos∠B′CE=cos∠CFD,求出CP的长.
如图,作点B关于AC的对称点B′,过点B′作B′E⊥BC于E,交AC于P,连接CB′交AD于F,连接BP,
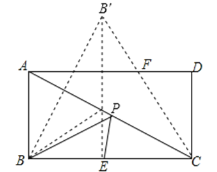
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCA=∠FAC,
∵点B关于AC的对称点是B′,
∴∠FCA=∠BCA,
∴∠FAC=∠FCA,
∴FA=FC.
令FA=x,则FC=x,FD=4-x.
在Rt△CDF中,∵FC2=FD2+CD2,
∴x2=(4-x)2+32,
∴x=![]() ,
,
∵cos∠B′CE=cos∠CFD,
∴CE:B′C=DF:CF,
∴CE:4=![]() :
:![]() ,
,
∴CE=![]() ,
,
∴B′E=![]() ,
,
∴BE+EF的最小值为=![]() .
.

练习册系列答案
相关题目