题目内容
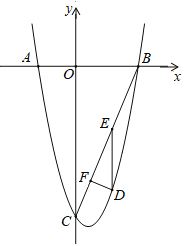
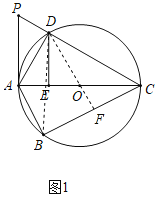
【题目】如图1,四边形ABCD内接于圆O,AC是圆O的直径,过点A的切线与CD的延长线相交于点P.且∠APC=∠BCP.
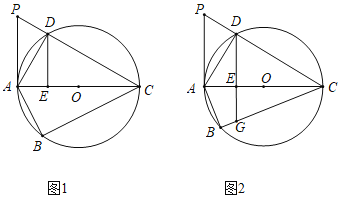
(1)求证:∠BAC=2∠ACD.
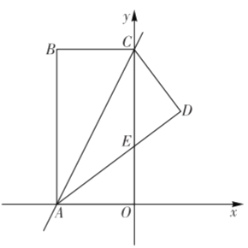
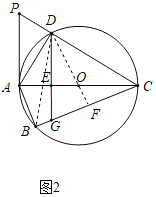
(2)过图1中的点D作DE⊥AC于E,交BC于G(如图2),BG:GE=3:5,OE=5,求⊙O的半径.
【答案】(1)证明见解析;(2)⊙O的半径为13.
【解析】
(1)连接BD,作DF⊥BC于F,由切线的性质得出∠PAC=90°,由圆周角定理得出∠ADC=90°,证出∠APC=∠DAC=∠DBC,得出∠DBC=∠BCP,证出BD=CD,由等腰三角形的性质和垂径定理得出BF=CF=![]() BC,D、O、F三点共线,∠CDF=
BC,D、O、F三点共线,∠CDF=![]() ∠BDC,由圆周角定理和等腰三角形的性质即可得出结论;
∠BDC,由圆周角定理和等腰三角形的性质即可得出结论;
(2)设BG=3x,则GE=5x,证明△DEC≌△CFD(AAS),得出DE=CF,CE=DF,求出OE=OF=5,证明△GDF≌△GCE(ASA),得出GF=GE=5x,得出DE=CF=BF=BG+GF=8x,DG=DE+GE=13x,由勾股定理得出DF=![]() =12x,证明△ODE∽△GDF,得出
=12x,证明△ODE∽△GDF,得出![]() =
=![]() ,解得x=
,解得x=![]() ,进而得出答案.
,进而得出答案.
证明:(1)连接BD,作DF⊥BC于F,如图1所示:
∵PA是⊙O的切线,
∴PA⊥AC,
∴∠PAC=90°,
∴∠APC+∠ACP=90°,
∵AC是圆O的直径,
∴∠ADC=90°,
∴∠DAC+∠ACP=90°,
∴∠APC=∠DAC=∠DBC,
∵∠APC=∠BCP,
∴∠DBC=∠BCP,
∴BD=CD,
∵DF⊥BC,
∴BF=CF=![]() BC,D、O、F三点共线,
BC,D、O、F三点共线,
∴∠CDF=![]() ∠BDC,
∠BDC,
∵∠BDC=∠BAC,
∴∠BAC=2∠CDF,
∵OD=OC,
∴∠CDF=∠ACD,
∴∠BAC=2∠ACD;
解:(2)∵BG:GE=3:5,
∴设BG=3x,则GE=5x,
∵DE⊥AC,
∴∠DEC=90°=∠CFD,
在△DEC和△CFD中,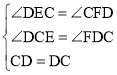 ,
,
∴△DEC≌△CFD(AAS),
∴DE=CF,CE=DF,
∴OE﹣OC=DF﹣OD,即OE=OF=5,
∵∠DGF+∠GDF=∠DGF+∠GCE=90°,
∴∠GDF=∠GCE,
在△GDF和△GCE中,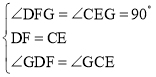 ,
,
∴△GDF≌△GCE(ASA),
∴GF=GE=5x,
∴DE=CF=BF=BG+GF=3x+5x=8x,
∴DG=DE+GE=13x,
∴DF=![]() =
=![]() =12x,
=12x,
∵∠ODE=∠GDF,∠DEO=∠DFG=90°,
∴△ODE∽△GDF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:x=![]() ,
,
∴DF=12×![]() =18,
=18,
∴OD=DF﹣OF=18﹣5=13,
即⊙O的半径为13.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |

A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.