Question

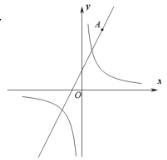
【题目】如图，在平面直角坐标系内，为坐标原点，点为直线上一动点，过作轴，交轴于点（点在原点右侧），交双曲线于点，且，则当存在时，其面积为__________．

Answer 1

【答案】1

【解析】

根据点A在一次函数图像上，因此设点A(a，2a+1)，点B在反比例函数图像上，则点B(a， )，就可得到AC，BC的长，再根据AC+BC=4，建立关于a的方程，解方程求出a的值，由题意可得到符合题意的a的值，然后利用三角形的面积公式可求解.

由点A在直线y=2x+1上，可设点A(a，2a+1) （a＞0），

由点B在直线y=上，AB⊥x轴，可得点B(a， )，

∴AC=2a+1，BC=，

∵AC+BC=4，

∴2a+1+=4，即2a2-3a+1=0，

解得：a1=，a2=1，

∴A(1，3)，B(1，1)或A( ，2)，B(，2)，

由题意△OAB存在， 所以A( ，2)，B(，2)舍去，

∴S△OAB=AB·xA=×2×1=1.

故答案为1.