题目内容
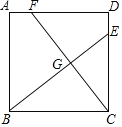
【题目】如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
证明△BCE≌△CDF(SAS),得∠CBE=∠DCF,所以∠CGE=90°,根据等角的余弦可得CG的长,可得结论.
正方形ABCD中,∵BC=4,
∴BC=CD=AD=4,∠BCE=∠CDF=90°,
∵AF=DE=1,
∴DF=CE=3,
∴由勾股定理可求得:BE=CF=5,
在△BCE和△CDF中,
 ,
,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF,
∵∠CBE+∠CEB=∠ECG+∠CEB=90°=∠CGE,
cos∠CBE=cos∠ECG=![]() ,
,
∴![]() ,CG=
,CG=![]() ,
,
∴GF=CF﹣CG=5﹣![]() =
=![]() ,
,
故选:A.

练习册系列答案
相关题目