题目内容
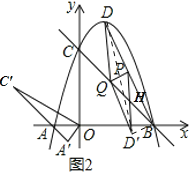
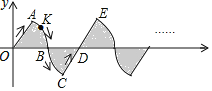
【题目】如图1,已知抛物线![]() 与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
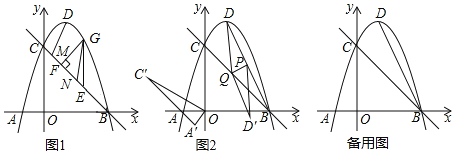
![]() 点G是直线BC上方抛物线上一动点
点G是直线BC上方抛物线上一动点![]() 不与B、C重合
不与B、C重合![]() ,过点G作y轴的平行线交直线BC于点E,作
,过点G作y轴的平行线交直线BC于点E,作![]() 于点F,点M、N是线段BC上两个动点,且
于点F,点M、N是线段BC上两个动点,且![]() ,连接DM、
,连接DM、![]() 当
当![]() 的周长最大时,求
的周长最大时,求![]() 的最小值;
的最小值;
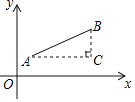
![]() 如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将
如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将![]() 沿PQ翻折,且线段
沿PQ翻折,且线段![]() 的中点恰好落在线段BQ上,将
的中点恰好落在线段BQ上,将![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 得到
得到![]() ,点T为坐标平面内一点,当以点Q、
,点T为坐标平面内一点,当以点Q、![]() 、
、![]() 、T为顶点的四边形是平行四边形时,求点T的坐标.
、T为顶点的四边形是平行四边形时,求点T的坐标.
【答案】(1)![]() 最小值为
最小值为![]() ;(2)点T的坐标为
;(2)点T的坐标为![]() 或
或![]() 或
或![]()
【解析】
![]() 先求出点B、C、D的坐标,可求直线BC解析式且得到
先求出点B、C、D的坐标,可求直线BC解析式且得到![]() 由
由![]() 轴和
轴和![]() 可得
可得![]() 是等腰直角三角形,则GE最大时其周长最大
是等腰直角三角形,则GE最大时其周长最大![]() 设点G坐标为
设点G坐标为![]() ,则点
,则点![]() ,可列得GE与a的函数关系式,配方可求出其最大值,得到此时的G坐标和EF的长,即得到MN长
,可列得GE与a的函数关系式,配方可求出其最大值,得到此时的G坐标和EF的长,即得到MN长![]() 求
求![]() 最小值转化为求
最小值转化为求![]() 最小值
最小值![]() 先作D关于直线BC的对称点
先作D关于直线BC的对称点![]() ,再通过平移
,再通过平移![]() 得
得![]() ,构造“将军饮马”的基本图形求解.
,构造“将军饮马”的基本图形求解.
![]() 由翻折得DD′⊥PQ,PD=PD′,再由P为BD中点证得∠BD′D=90°,得PQ//BD′,又D′P中点H在BQ上,可证
由翻折得DD′⊥PQ,PD=PD′,再由P为BD中点证得∠BD′D=90°,得PQ//BD′,又D′P中点H在BQ上,可证![]() ≌△D′BH,所以有D′Q//BP,即四边形DQ D′P为菱形,得
≌△D′BH,所以有D′Q//BP,即四边形DQ D′P为菱形,得![]() 设Q点坐标为
设Q点坐标为![]() 即可列方程求得
即可列方程求得![]() 再根据题意把点A′、C′求出
再根据题意把点A′、C′求出![]() 以点Q、
以点Q、![]() 、
、![]() 、T为顶点的四边形是平行四边形,要进行分类讨论,结合图形,利用平行四边形对边平行的性质,用平移坐标的方法即可求得点T.
、T为顶点的四边形是平行四边形,要进行分类讨论,结合图形,利用平行四边形对边平行的性质,用平移坐标的方法即可求得点T.
![]() ,
,
![]() 抛物线与x轴交于点
抛物线与x轴交于点![]() 、点
、点![]() ,与y轴交于点
,与y轴交于点![]() ,顶点
,顶点![]() ,
,
![]() 直线CB解析式:
直线CB解析式:![]() ,
,![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
![]() ,
,
设点![]() ,则点
,则点![]() ,其中
,其中![]() ,
,
![]() ,
,
![]() 时,GE有最大值为
时,GE有最大值为![]() ,
,
![]() 的周长最大时,
的周长最大时,![]() ,
,![]() ,
,
![]() ,E点可看作点F向右平移
,E点可看作点F向右平移![]() 个单位、向下平移
个单位、向下平移![]() 个单位,
个单位,
如图1,作点D关于直线BC的对称点![]() ,过N作
,过N作![]() 且
且![]() ,
,
![]() ,
,![]() 即
即![]()
![]() ,
,
![]() 当
当![]() 、N、G在同一直线上时,
、N、G在同一直线上时,![]() 为最小值,
为最小值,
![]() ,
,
![]() 最小值为
最小值为![]() ;
;
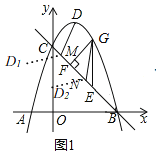
![]() 连接DD′、D′B,设D′P与BQ交点为
连接DD′、D′B,设D′P与BQ交点为![]() 如图
如图![]() ,
,
![]() 沿PQ翻折得△D′PQ,
沿PQ翻折得△D′PQ,
∴DD′⊥PQ,PD=PD′,DQ=D′Q,∠DQP=∠D′QP,
![]() 为BD中点,
为BD中点,
∴PB=PD=PD′,![]() ,
,
∴△BDD′是直角三角形,∠BD′D=90°,
∴PQ//BD′,
∴∠PQH=∠D′BH,
![]() 为D′P中点,
为D′P中点,
∴PH=D′H,
在![]() 与△D′BH中
与△D′BH中
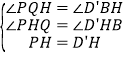 ,
,
![]() ≌△D′BH (AAS),
≌△D′BH (AAS),
∴PQ=BD′,
![]() 四边形BPQD′是平行四边形,
四边形BPQD′是平行四边形,
∴D′Q//BP,
∴∠DPQ=∠D′QP,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
解得:![]() ,
,![]() 舍去
舍去![]() ,
,
![]() 点Q坐标为
点Q坐标为![]() ,
,
![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 得到
得到![]() ,
,
∴A′![]() ,C′
,C′![]() ,
,
∴A′、C′横坐标差为![]() ,纵坐标差为
,纵坐标差为![]() ,
,
A′、Q横坐标差为![]() ,纵坐标差为
,纵坐标差为![]() ,
,
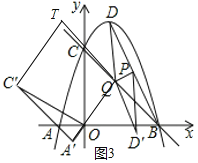
当有平行四边形A′C′TQ时![]() 如图
如图![]() ,点T横坐标为
,点T横坐标为![]() ,纵坐标为
,纵坐标为![]() ;
;
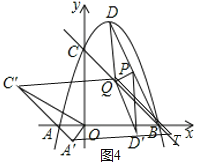
当有平行四边形A′C′QT时![]() 如图
如图![]() ,点T横坐标为
,点T横坐标为![]() ,纵坐标为
,纵坐标为![]() ;
;
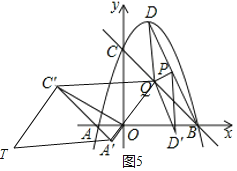
当有平行四边形A′TC′Q时![]() 如图
如图![]() ,点T横坐标为
,点T横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,
综上所述,点T的坐标为![]() 或
或![]() 或
或![]() .
.