题目内容
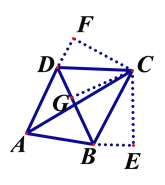
【题目】如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( )

A. α B. ![]() α C. 90﹣α D. 90﹣
α C. 90﹣α D. 90﹣![]() α
α
【答案】C
【解析】分析:作CE⊥AB交AB的延长线于点E,作CF⊥AD交AD的延长线于点F,作CG⊥AB交BD于点G,由“AAS”证明△CBE≌△CBG,再由“HL”证明△CDG≌△CDF,得到∠CDG=∠CDF,由三角形内角和、外角和表示出∠FDB,进而可求出∠BDC的度数.
详解:作CE⊥AB交AB的延长线于点E,作CF⊥AD交AD的延长线于点F,作CG⊥AB交BD于点G.
∵∠ABD=52°,∠ABC=116°,
∴∠CBE=180-116=64, ∠CBD=116-52=64,
∴∠CBE=∠CBD.
在△CBE和△CBG中,
∵∠CBE=∠CBD,
∠E=∠CGB=90,
BC=BC,
∴△CBE≌△CBG,
∴CE=CG.
∵AC平分∠DAB,CG⊥AB,CE⊥AB,
∴CE=CF,
∴CG=CF.
在△CDG和△△CDF中,
∵CG=CF,
CD=CD,
∴△CDG≌△CDF,
∴∠CDG=∠CDF.
∵∠ABC=116°,∠ACB=α°,
∴∠CAB=180-116-α=64 -α,
∵AC平分∠DAB,
∴∠DAB=2(64 -α)=128-2α,
∴∠FDB=128-2α+52=180-2α,
∴∠BDC=![]() (180+2α)=90-α.
(180+2α)=90-α.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目