题目内容
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
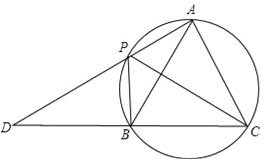
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=![]() ,求PD的长.
,求PD的长.
【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)由圆周角定理可知∠ABC=∠BAC=60°,从而可证得△ABC是等边三角形;
(2)由△ABC是等边三角形可得出“AC=BC=AB=![]() ,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
试题解析:(1)∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC是等边三角形;
(2)∵△ABC是等边三角形,AB=![]() ,∴AC=BC=AB=
,∴AC=BC=AB=![]() ,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=
,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=![]() ,∴AP=ACcot∠APC=2.在Rt△DAC中,∠DAC=90°,AC=
,∴AP=ACcot∠APC=2.在Rt△DAC中,∠DAC=90°,AC=![]() ,∠ACD=60°,∴AD=ACtan∠ACD=6,∴PD=AD﹣AP=6﹣2=4.
,∠ACD=60°,∴AD=ACtan∠ACD=6,∴PD=AD﹣AP=6﹣2=4.

练习册系列答案
相关题目