��Ŀ����
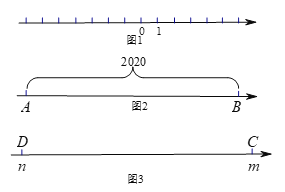
����Ŀ����֪����ֽ������һ����(��ͼ1)���۵���ֽ�森
��1������ʾ1�ĵ����ʾ��1�ĵ��غϣ����ʾ��7�ĵ����ʾ �ĵ��غϣ�
��2������ʾ��2�ĵ����ʾ6�ĵ��غϣ��ش���������:
�ٱ�ʾ12�ĵ����ʾ �ĵ��غϣ�
����ͼ2����������AB����֮��ľ���Ϊ2020(��A�ڵ�B�����)����AB���㾭�۵����غϣ���AB�����ʾ�����ֱ��� ��
��3����ͼ3����m��n��ʾ�ĵ�C�͵�D���۵����غ�(m��n)���ۺ�������Ľ���Ϊ�ۺ۵㣮��֪�߶�CD������P��Q (��P�ڵ�Q����࣬PQ��CD)��PQ��a�����߶�PQ�Ķ˵����ۺ۵��غ�ʱ����PQ�����ʾ�����ֱ��Ƕ���?(�ú�m��n��a�Ĵ���ʽ��ʾ)��
���𰸡���1��![]() ����2����-8����-1008 ��1012 ����3����PΪ�ۺ۵㣬��P:
����2����-8����-1008 ��1012 ����3����PΪ�ۺ۵㣬��P:![]() �� Q:
�� Q:![]() ����QΪ�ۺ۵㣬��P:
����QΪ�ۺ۵㣬��P:![]() �� Q:
�� Q:![]() .
.
��������
��1����������ʾ1�ĵ����ʾ��1�ĵ��غ����ҳ��Գ��ᣬ���ɵó��𰸣�
��2���ٸ�������ʾ��2�ĵ����ʾ6�ĵ��غ����ҳ��Գ��ᣬ���ɵó��𰸣��ڸ��ݶԳ���������Գ������Ϊ1010�ĵ㼴�ɵó��𰸣�
��3�����ݣ�2���ļ��㷽�����㼴�ɵó���.
�⣺��1��������ɵã�ԭ��Ϊ�Գ��ᣬ�ʴ�Ϊ��7 ��
��2����������ɵã�2Ϊ�Գ��ᣬ�ʴ�Ϊ��-8��
�ڡ߶Գ���Ϊ2
��2����Ϊ1010�ĵ�Ϊ��-1008��1012
�ֵ�A�ڵ�B�����
���A��ʾ����Ϊ-1008����B��ʾ����Ϊ1012��
��3����������ɵã��ۺ۵�Ϊ![]()
����PΪ�ۺ۵㣬��P:![]() ��Q:
��Q:![]()
����QΪ�ۺ۵㣺��P:![]() ��Q:
��Q:![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�