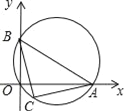
题目内容
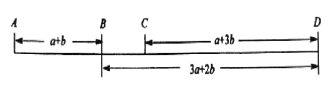
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)过点O作OG⊥DC,垂足为G.先证明∠OAD=90°,从而得到∠OAD=∠OGD=90°,然后利用AAS可证明△ADO≌△GDO,则OA=OG=r,则DC是⊙O的切线;
(2)连接OF,依据垂径定理可知BE=EF=12,在Rt△OEF中,依据勾股定理可知求得OF=13,然后可得到AE的长,最后在Rt△ABE中,利用锐角三角函数的定义求解即可.
试题解析:
(1)证明:
过点O作OG⊥DC,垂足为G.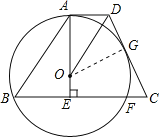
∵AD∥BC,AE⊥BC于E,
∴OA⊥AD.
∴∠OAD=∠OGD=90°.
在△ADO和△GDO中
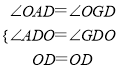 ,
,
∴△ADO≌△GDO.
∴OA=OG.
∴DC是⊙O的切线.
(2)如图所示:连接OF.
∵OA⊥BC,
∴BE=EF=![]() BF=12.
BF=12.
在Rt△OEF中,OE=5,EF=12,
∴OF=![]() ,
,
∴AE=OA+OE=13+5=18.
∴tan∠ABC=![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?