Question

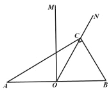
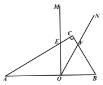
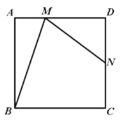
【题目】如图，在边长为 a 的正方形 ABCD 中， M 是边 AD 上一动点（点 M 与点 A 、 D 不重合）， N 是 CD 的中点，且CBMNMB ，则 tan ABM （___________）

Answer 1

【答案】

【解析】

延长MN交BC延长线于点E. 设MD=x.证DMN≌△△CEN (AAS)，得MD=CE，MN=EN.

得BE=EM=a+x，MN= ，在Rt△MDN中,由MD2+ND2=MN2，得x2+=()2,解得x= ，得AM=ADMD=a-=，所以,tan∠ABM=.

如图，

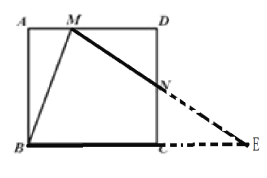
延长MN交BC延长线于点E. 设MD=x.

∵∠MBC=∠BMN，

∴EB=EM.

∵四边形ABCD是正方形，

∴AD∥BC，

∴∠DMN=∠E，

在△DMN和△ECN中,

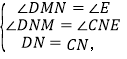
∴DMN≌△△CEN (AAS)

∴MD=CE，MN=EN.

∴BE=EM=a+x，

∴MN=

在Rt△MDN中,

∵MD2+ND2=MN2，

∴x2+=()2,解得x=

∴AM=ADMD=a-=

在Rt△ABM中,tan∠ABM=.