题目内容
【题目】如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点,
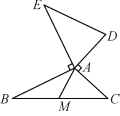
求证:DE=2AM.
【答案】见解析.
【解析】
延长AM至N,使MN=AM,证△AMC≌△NMB,推出AC=BN=AD,求出∠EAD=∠ABN,证△EAD≌△ABN即可.
延长AM至N,使MN=AM,连接BN,
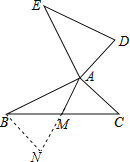
∵点M为BC的中点,
∴CM=BM,
在△AMC和△NMB中
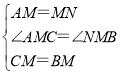
∴△AMC≌△NMB(SAS),
∴AC=BN,∠C=∠NBM,
∵AB⊥AE,AD⊥AC,
∴∠EAB=∠DAC=90°,
∴∠EAD+∠BAC=180°,
∴∠ABN=∠ABC+∠C=180゜-∠BAC=∠EAD,
在△EAD和△ABN中
∵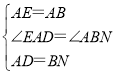 ,
,
∴△ABN≌△EAD(SAS),
∴DE=AN=2MN.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目