题目内容
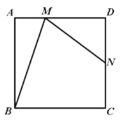
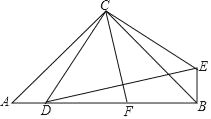
【题目】已知,如图,在 ABC 中, ACB 90, B 60, BC 2 ,MON 30.
(1)如图 1, MON 的边 MO ⊥ AB ,边 ON 过点 C ,求 AO 的长;
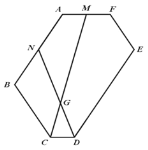
(2)如图 2,将图 1 中的 MON 向右平移,MON 的两边分别与 ABC 的边 AC 、BC
相交于点 E 、 F ,连接 EF ,若 OEF 是直角三角形,求 AO 的长;
(3)在(2)的条件下,MON 与 ABC 重叠部分面积是否存在最大值,若存在,求出 最大值,若不存在,请说明理由.
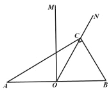
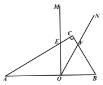
图 1 图 2 备用图
【答案】(1)2;(2) ![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先证△BOC是等边三角形,得BO=2,在![]() 中,
中,![]() ,
,![]() ,得AB=4.所以AO=AB-BO=2;
,得AB=4.所以AO=AB-BO=2;
(2)分两种情况①∠OEF=90°,设AO=![]() ,根据题意得
,根据题意得![]() ;②∠OFE=90°
;②∠OFE=90°
设AO=![]() ,根据题意得
,根据题意得![]() ;
;
(3)设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,根据题意得:
,根据题意得:![]() ,即
,即![]() ,求二次函数的最值可得.
,求二次函数的最值可得.
(1)∴∠MON=30°,MO⊥AB,
∴∠COB=60°,
∵∠B=60°,
∴△BOC是等边三角形,
∵BC=2,
∴BO=2,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴AB=4.
∴ AO=AB-BO=2.
(2)①∠OEF=90°
设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,
,![]() ,
,
∴![]() ∴
∴![]()
②∠OFE=90°
设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]() 是直角三角形时,AO长为
是直角三角形时,AO长为![]() 或
或![]()
(3)设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,
,
设重叠部分的面积为S,根据题意得:![]()
∴![]()
整理得:![]()
∵![]() ,
,
∴![]() 有最大值
有最大值
∴当![]() 时,
时,![]() 最大值
最大值![]()

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目