题目内容
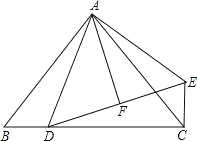
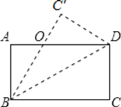
【题目】已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;
(2)若AD=6,CE=4,求AC的长?

【答案】(1)证明见解析;(2)AC=10.
【解析】
(1)由题意∠BAC+∠BCA=120°,根据∠AFC=180﹣∠FAC﹣∠FCA=180﹣![]() =120°,即可解决问题;(2)在AC上截取AG=AD=6,连接FG.只要证明△ADF≌△AGF(SAS),推出∠AFD=∠AFG=60°,∠GFC=∠CFE=60°,再证明△CGF≌△CEF(ASA),推出CG=CE=4,由此即可解决问题.
=120°,即可解决问题;(2)在AC上截取AG=AD=6,连接FG.只要证明△ADF≌△AGF(SAS),推出∠AFD=∠AFG=60°,∠GFC=∠CFE=60°,再证明△CGF≌△CEF(ASA),推出CG=CE=4,由此即可解决问题.
(1)∵AE、CD分别为△ABC的角平分线,
∴∠FAC=![]() ,∠FCA=
,∠FCA=![]() ,
,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180﹣∠FAC﹣∠FCA=180°﹣![]() ×120°=120°.
×120°=120°.
(2)在AC上截取AG=AD=6,连接FG.
∵AE、CD分别为△ABC的角平分线
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中
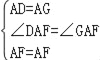 ,
,
∴△ADF≌△AGF(SAS)
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中
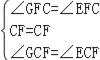 ,
,
∴△CGF≌△CEF(ASA),
∴CG=CE=4,
∴AC=10.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目