题目内容
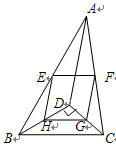
如图，正方形ABCD的边长为4，P为对角线AC上一点，且CP = 3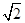
，PE⊥PB交CD于点E，则PE =____________.
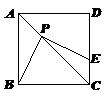
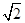，PE⊥PB交CD于点E，则PE =____________.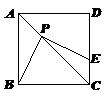
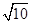
连接BE，设CE的长为x
∵AC为正方形ABCD的对角线，正方形边长为4，CP=3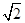
∴∠BAP=∠PCE=45°，AP=4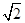-3=
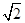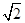
∴BP2=AB2+AP2-2AB×AP×cos∠BAP=42+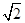（）2-2×4××
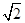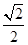=10
PE2=CE2+CP2-2CE×CP×cos∠PCE=（3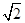）2+x2-2x×3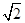×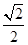=x2-6x+18
BE2=BC2+CE2=16+x2 在Rt△PBE中，BP2+PE2=BE2，即：10+x2-6x+18=16+x2，解得：x=2
∴PE2=22-6×2+18=10 ∴PE=．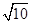
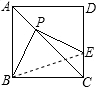
∵AC为正方形ABCD的对角线，正方形边长为4，CP=3
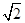
∴∠BAP=∠PCE=45°，AP=4
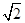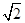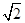
-3=∴BP2=AB2+AP2-2AB×AP×cos∠BAP=42+（
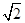）2-2×4×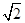×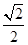=10PE2=CE2+CP2-2CE×CP×cos∠PCE=（3
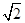）2+x2-2x×3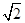×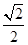=x2-6x+18BE2=BC2+CE2=16+x2 在Rt△PBE中，BP2+PE2=BE2，即：10+x2-6x+18=16+x2，解得：x=2
∴PE2=22-6×2+18=10 ∴PE=
．
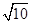练习册系列答案
相关题目
；
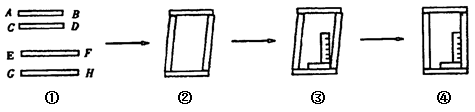
是四边形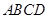
的对角线
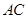上两点，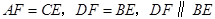
．
；
