题目内容
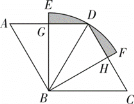
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=4,以点B为圆心,BD长为半径的扇形EBF与AD,CD交于点G,H,且G,H分别为AD,CD边上的中点,则阴影部分的面积为____.
【答案】![]() -4
-4![]()
【解析】
在菱形ABCD中,∠BAD=60°,可得△ABD和△BDC是等边三角形,得AD=BD=AB=DC=4,根据G,H分别为AD,CD边上的中点,可得BG⊥AD,BH⊥DC,AG=DG=DH=CH=2,进而求得BG=BH=2![]() ,再根据阴影部分面积等于扇形EBF的面积减去两个三角形的面积即可求解.
,再根据阴影部分面积等于扇形EBF的面积减去两个三角形的面积即可求解.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠BCD=∠BAD
又∵∠BAD=60°,
∴△ABD和△BDC是等边三角形,
∴AD=BD=AB=DC=4,
∵G,H分别为AD,CD边上的中点,
∴BG⊥AD,BH⊥DC,AG=DG=DH=CH=2,
∴∠DBG=∠DBH=30°,
∴BG=BH=2![]() ,
,
∴∠EBF=60°,
∴S阴影=S扇形EBF-S△BGD-S△BHD
=![]()
=![]() -4
-4![]() .
.
故答案为:![]() -4
-4![]() .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目