题目内容
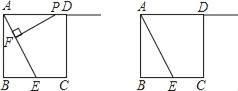
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(3)试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.
【答案】(1)证明见解析;(2)满足条件的x的值为2或5;(3)当x=4-![]() 或x=4+
或x=4+![]() 或8<x≤4+2
或8<x≤4+2![]() 时,⊙D与线段AE只有一个公共点.
时,⊙D与线段AE只有一个公共点.
【解析】
(1)根据正方形的性质和PF⊥AE易证三角形相似.
(2)由于对应关系不确定,所以应针对不同的对应关系分情况考虑:当∠PEF=∠EAB时,则得到四边形ABEP为矩形,从而求得x的值;当∠PEF=∠AEB时,再结合△PFA∽△ABE,得到等腰△APE.再根据等腰三角形的三线合一得到F是AE的中点,运用勾股定理和相似三角形的性质进行求解.
(3)此题首先应针对点P的位置分为两种大情况:点P在AD边上时或当点P在AD的延长线上时.同时还要特别注意⊙D与线段AE只有一个公共点,不一定必须相切,只要保证和线段AE只有一个公共点即可.故求得相切时的情况和相交,但其中一个交点在线段AE外的情况即是x的取值范围.
(1)证明:∵正方形ABCD,
∴AD∥BC.
∴∠ABE=90°.
∴∠PAF=∠AEB.
又∵PF⊥AE,
∴∠PFA=∠ABE=90°.
∴△PFA∽△ABE.
(2)解:情况1,当△EFP∽△ABE,且∠PEF=∠EAB时,
则有PE∥AB
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
情况2,当△PFE∽△ABE,且∠PEF=∠AEB时,
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵![]() =
=![]() =
=![]() =
=![]() ,
,
∴EF=![]() AE=
AE=![]() .
.
∵![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
(3)解:如图,
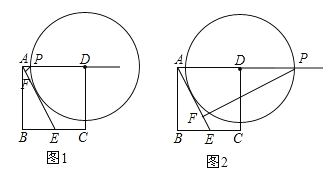
作DH⊥AE,则⊙D与线段AE的距离d即为DH的长,可得d=![]()
当点P在AD边上时,⊙D的半径r=DP=4﹣x;
当点P在AD的延长线上时,⊙D的半径r=DP=x﹣4;
如图1时,⊙D与线段AE相切,此时d=r,即![]() =4-x,∴x=4-
=4-x,∴x=4-![]() ;
;
如图2时,⊙D与线段AE相切,此时d=r,即![]() =x-4,∴x=4+
=x-4,∴x=4+![]() ;
;
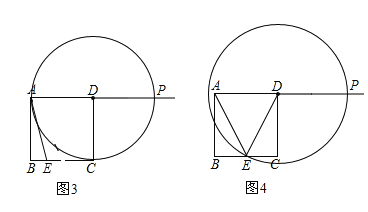
如图3时,DA=PD,则PA=x=2DA=8
如图4时,当PD=ED时,
∵DE=![]() =2
=2![]() ,
,
∴PA=PD+AD=4+2![]() ,
,
∴当x=4-![]() 或x=4+
或x=4+![]() 或8<x≤4+2
或8<x≤4+2![]() 时,⊙D与线段AE只有一个公共点.
时,⊙D与线段AE只有一个公共点.

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案