题目内容
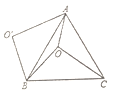
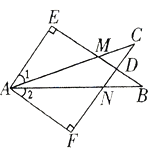
【题目】如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.
(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;
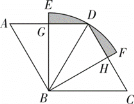
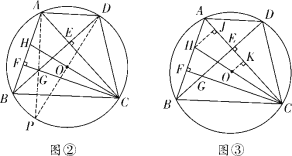
(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=![]() ,求线段AH长
,求线段AH长

【答案】(1)见解析;(2)![]()
【解析】
(1)过点E作EF的垂线交CF于点I,证△EFI是等腰直角三角形,进而可证△AEF≌△GEI,等量代换即可证明结论;
(2)连接DO并延长,交⊙O于点P,连接AP,先求出圆的半径,再过点H作HJ⊥AC于点J,过点O作OK⊥AC于点K,根据三角函数可设设AJ=3t,则HJ=4t,由勾股定理可知AH=5t,根据角平分线的性质定理及三角函数用含有t的代数式表示出HF=HJ=4t,AF=9t,CF=CJ=12t,AC=15t,CK=![]() t,再根据平行线分线段成比例定理及勾股定理求解即可.
t,再根据平行线分线段成比例定理及勾股定理求解即可.
(1)如图,过点E作EF的垂线交CF于点I,
∵CF⊥AB,
∴∠AFG=90°,
∵EF平分∠AFG,
∴∠EFI=45°,
∵EF⊥EI,
∴∠EIF=45°,
∴EF=EI
又∵∠EGF+∠FAE=180°,∠EGF+∠EGI=180°,
∴∠EGI=∠FAE,
∵∠AEB=∠FEI=90°,
∴∠AEF=∠GEI,
∴△AEF≌△GEI(AAS),
∴AE=GE
(2)如图②,连接DO并延长,交⊙O于点P,连接AP,
则∠ABD=∠P,
∵DP为⊙O的直径,
∴∠PAD=90°,
∵tan∠FBG=![]() ,
,
∴tanP=![]() =
=![]() ,
,
又∵AD=3,
∴AP=4,PD=5,
∴OD=![]()
∴OC=OD=![]()
如图③,过点H作HJ⊥AC于点J,过点O作OK⊥AC于点K,
∵HJ⊥AC,BD⊥AC,
∴HJ∥BD,
∴∠ABD=∠AHJ,则tan∠AHJ=![]() ,
,
设AJ=3t,则HJ=4t,由勾股定理可知AH=5t,
∵CH是∠ACF的平分线,且HF⊥CF,HJ⊥AC,
∴HF=HJ=4t,
∴AF=AH+HF=9t,
设CF=x,则CJ=x,
∵∠BFG=∠GEC,∠FGB=∠EGC,
∴∠FBG=∠ECG,
∴tan∠FCJ=![]() =
=![]() =
=![]() ,
,
解得x=12t,
∴CF=CJ=12t,
∴AC=15t,
∴CK=![]() t
t
又∵OK∥HJ,
∴![]() =
=![]() ,
,
∴OK=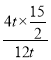 =
=![]() t,
t,
∴在Rt△OCK中,OK2+KC2=OC2,即(![]() t)2+(
t)2+(![]() t)2=(
t)2=(![]() )2,
)2,
解得t=![]() (负值舍去),
(负值舍去),
∴AH=5t=![]()

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案