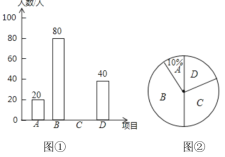
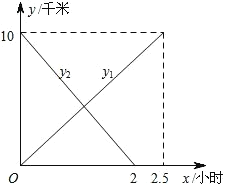
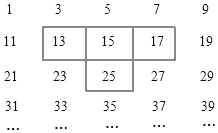
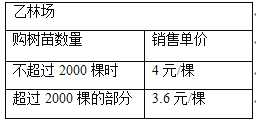
题目内容
【题目】为改善生态环境,防止水土流失,某村计划在堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
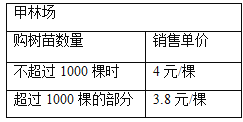
设购买白杨树苗x棵,到两家林场购买所需费用分别为![]() (元)、
(元)、![]() (元). 则:
(元). 则:
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
【答案】(1)5900,6000;
(2)y甲=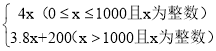 ;y乙=
;y乙=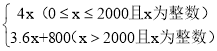 ;
;
(3)当0≤x≤1000或x=3000时,两家林场购买一样,
当1000<x<3000时,到甲林场购买合算;
当x>3000时,到乙林场购买合算.
【解析】
(1)根据购买树苗需要的费用=树苗的单价×数量分别计算甲、乙的费用;
(2)根据购买树苗需要的费用=树苗的单价×数量,分别求出当0≤x≤1000,或x>1000时,y甲与x之间的函数关系式;当.0≤x≤2000,或x>2000时y乙与x之间的函数关系式;
(3)分类讨论,当0≤x≤1000,1000<x≤2000时,x>2000时,根据y甲、y乙的关系式列出不等式或方程,即可得结论.
解:(1)由题意,得.
y甲=4×1000+3.8(1500﹣1000)=5900元,
y乙=4×1500=6000元;
故答案为:5900,6000;
(2)当0≤x≤1000时,
y甲=4x,
x>1000时.
y甲=4000+3.8(x﹣1000)=3.8x+200,
∴y甲=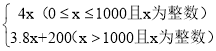 ;
;
当0≤x≤2000时,
y乙=4x
当x>2000时,
y乙=8000+3.6(x﹣2000)=3.6x+800
∴y乙=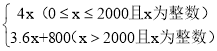 ;
;
(3)由题意,得
当0≤x≤1000时,两家林场单价一样,
∴到两家林场购买所需要的费用一样.
当1000<x≤2000时,甲林场有优惠而乙林场无优惠,
∴当1000<x≤2000时,到甲林场优惠;
当x>2000时,y甲=3.8x+200,y乙=3.6x+800,
当y甲=y乙时
3.8x+200=3.6x+800,
解得:x=3000.
∴当x=3000时,到两家林场购买的费用一样;
当y甲<y乙时,
3.8x+200<3.6x+800,
x<3000.
∴2000<x<3000时,到甲林场购买合算;
当y甲>y乙时,
3.8x+200>3.6x+800,
解得:x>3000.
∴当x>3000时,到乙林场购买合算.
综上所述,当0≤x≤1000或x=3000时,两家林场购买一样,
当1000<x<3000时,到甲林场购买合算;
当x>3000时,到乙林场购买合算.