题目内容
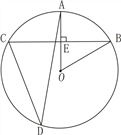
【题目】如图，在矩形
中，
，
相交于点
，
平分
交
于点
，若
，则
________．
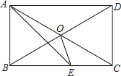
【答案】
【解析】
判断出△ABE是等腰直角三角形，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACB=30°，再判断出△ABO是等边三角形，根据等边三角形的性质求出OB=AB，再求出OB=BE，然后根据等腰三角形两底角相等求出∠BOE=75°，再根据∠AOE=∠AOB+∠BOE计算即可得解．
解：∵AE平分∠BAD，
∴∠BAE=∠DAE=45°，
∴∠AEB=45°，
∴△ABE是等腰直角三角形，
∴AB=BE，
∵∠CAE=15°，
∴∠ACE=∠AEB-∠CAE=45°-15°=30°，
∴∠BAO=90°-30°=60°，
∵矩形中OA=OB，
∴△ABO是等边三角形，
∴OB=AB，∠ABO=∠AOB=60°，
∴OB=BE，
∵∠OBE=∠ABC-∠ABO=90°-60°=30°，
∴∠BOE=
（180°-30°）=75°，
∴∠AOE=∠AOB+∠BOE，
=60°+75°，
=135°．
故答案为：135°．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
【题目】如图①是一张长为18
，宽为12的长方形硬纸板，把它的四个角都剪去一个边长为
的小正方形，然后把它折成一个无盖的长方体盒子（如图②），请回答下列问题：
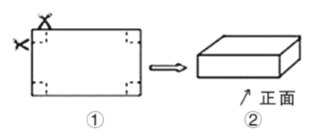
（1）折成的无盖长方体盒子的容积
；（用含
的代数式表示即可，不需化简）
（2）请完成下表，并根据表格回答，当取什么正整数时，长方体盒子的容积最大？
| 1 | 2 | 3 | 4 | 5 |
| 160 | ________ | 216 | ________ | 80 |
（3）从正面看折成的长方体盒子，它的形状可能是正方形吗？如果是正方形，求出的值；如果不是正方形，请说明理由．
